Abstract wave equation
Consider the Cauchy problem for the wave equation
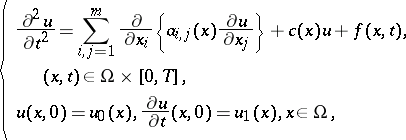 |
with the Dirichlet boundary conditions  or the Neumann boundary conditions
or the Neumann boundary conditions  ,
,  .
.
Here, 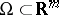 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary  ,
,  and
and  are smooth real functions on
are smooth real functions on  such that
such that 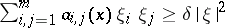 for all
for all 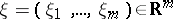 , with some fixed
, with some fixed 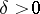 ;
; 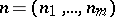 is the unit outward normal vector to
is the unit outward normal vector to 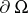 . Also,
. Also, 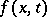 ,
,  ,
, 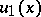 are given functions. The function
are given functions. The function 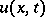 is the unknown function.
is the unknown function.
One can state this problem in the abstract form
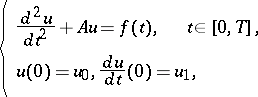 | (a1) |
which is considered in the Hilbert space 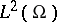 . Here,
. Here, 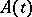 is the self-adjoint operator of
is the self-adjoint operator of 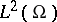 determined from the symmetric sesquilinear form
determined from the symmetric sesquilinear form
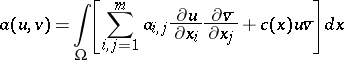 | (a2) |
on the space 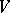 , see [a1], where
, see [a1], where 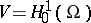 (respectively
(respectively 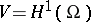 ) when the boundary conditions are Dirichlet (respectively, Neumann), by the relation
) when the boundary conditions are Dirichlet (respectively, Neumann), by the relation 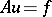 if and only if
if and only if 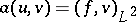 for all
for all 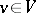 . There are several ways to handle this abstract problem.
. There are several ways to handle this abstract problem.
Let 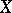 be a Banach space. A strongly continuous function
be a Banach space. A strongly continuous function 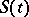 of
of 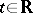 with values in
with values in  is called a cosine function if it satisfies
is called a cosine function if it satisfies 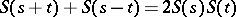 ,
, 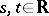 , and
, and 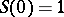 . Its infinitesimal generator
. Its infinitesimal generator  is defined by
is defined by 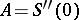 , with
, with 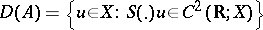 . The theory of cosine functions, which is very similar to the theory of semi-groups, was originated by S. Kurera [a2] and was developed by H.O. Fattorini [a3] and others.
. The theory of cosine functions, which is very similar to the theory of semi-groups, was originated by S. Kurera [a2] and was developed by H.O. Fattorini [a3] and others.
A necessary and sufficient condition for a closed linear operator  to be the generator of a cosine family is known. The operator determined by (a2) is easily shown to generate a cosine function which provides a fundamental solution for (a1).
to be the generator of a cosine family is known. The operator determined by (a2) is easily shown to generate a cosine function which provides a fundamental solution for (a1).
Suppose one sets 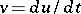 in (a1). Then one obtains the equivalent problem
in (a1). Then one obtains the equivalent problem
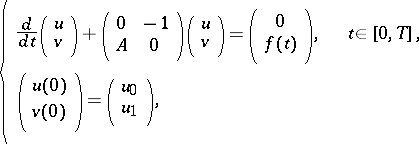 |
which is considered in the product space  . Since the equation is of first order, one can apply semi-group theory (see [a4], [a5]). Indeed, the operator
. Since the equation is of first order, one can apply semi-group theory (see [a4], [a5]). Indeed, the operator
 |
with its domain 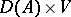 is the negative generator of a
is the negative generator of a 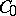 semi-group. The theory of semi-groups of abstract evolution equations provides the existence of a unique solution
semi-group. The theory of semi-groups of abstract evolution equations provides the existence of a unique solution 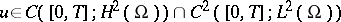 of (a1) for
of (a1) for 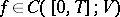 and
and 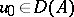 ,
, 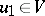 .
.
This method is also available for a non-autonomous equation
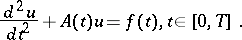 | (a3) |
In the case of Neumann boundary conditions, the difficulty arises that the domain of
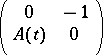 |
may change with 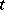 . One way to avoid this is to introduce the extension
. One way to avoid this is to introduce the extension 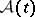 of
of 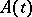 defined by
defined by 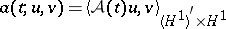 for all
for all  . Since
. Since  is a bounded operator from
is a bounded operator from 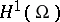 into
into 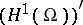 , the operator
, the operator
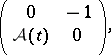 |
acting in 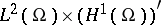 , has constant domain.
, has constant domain.
Another way is to reduce (a3) to
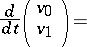 |
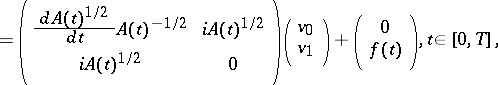 |
by setting  ,
, 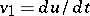 , under the assumption that
, under the assumption that 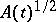 is strongly differentiable with values in
is strongly differentiable with values in 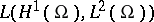 . Obviously, the linear operator of the coefficient has constant domain
. Obviously, the linear operator of the coefficient has constant domain 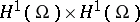 . Differentiability of the square root
. Differentiability of the square root 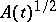 was studied in [a6], [a7].
was studied in [a6], [a7].
In order to consider in (a1) the case when 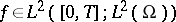 , one has to use the Lions–Magenes variational formulation. In this, one is concerned with the solution
, one has to use the Lions–Magenes variational formulation. In this, one is concerned with the solution  of the problem
of the problem
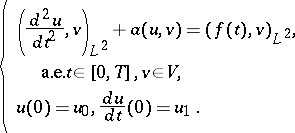 |
The existence of a unique solution 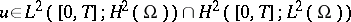 has been proved if
has been proved if 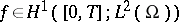 and
and 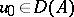 ,
, 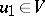 ; see [a8], Chap. 5.
; see [a8], Chap. 5.
This method is also available for a non-autonomous equation (a3).
The variational method enables one to take  from a wide class, an advantage that is very useful in, e.g., the study of optimal control problems. On the other hand, the semi-group method provides regular solutions, which is often important in applications to non-linear problems. Using these approaches, many papers have been devoted to non-linear wave equations.
from a wide class, an advantage that is very useful in, e.g., the study of optimal control problems. On the other hand, the semi-group method provides regular solutions, which is often important in applications to non-linear problems. Using these approaches, many papers have been devoted to non-linear wave equations.
References
| [a1] | J.-L. Lions, "Espaces d'interpolation et domaines de puissances fractionnaires d'opérateurs" J. Math. Soc. Japan , 14 (1962) pp. 233–241 |
| [a2] | S. Kurepa, "A cosine functional equation in Hilbert spaces" Canad. J. Math. , 12 (1960) pp. 45–50 |
| [a3] | H.O. Fattorini, "Ordinary differential equations in linear topological spaces II" J. Diff. Eq. , 6 (1969) pp. 50–70 |
| [a4] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
| [a5] | K. Yoshida, "Functional analysis" , Springer (1957) |
| [a6] | A. McIntosh, "Square roots of elliptic operators" J. Funct. Anal. , 61 (1985) pp. 307–327 |
| [a7] | A. Yagi, "Applications of the purely imaginary powers of operators in Hilbert spaces" J. Funct. Anal. , 73 (1987) pp. 216–231 |
| [a8] | J.-L. Lions, E. Magenes, "Problèmes aux limites non homogènes et applications" , 1–2 , Dunod (1968) |
Abstract wave equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abstract_wave_equation&oldid=17290