Laurent series
A generalization of a power series in non-negative integral powers of the difference 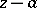 or in non-positive integral powers of
or in non-positive integral powers of 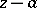 in the form
in the form
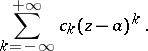 | (1) |
The series (1) is understood as the sum of two series:
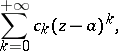 |
the regular part of the Laurent series, and
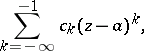 |
the principal part of the Laurent series. The series (1) is assumed to converge if and only if its regular and principal parts converge. Properties of Laurent series: 1) if the domain of convergence of a Laurent series contains interior points, then this domain is a circular annulus 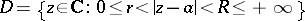 with centre at the point
with centre at the point 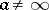 ; 2) at all interior points of the annulus of convergence
; 2) at all interior points of the annulus of convergence 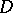 the series (1) converges absolutely; 3) as for power series, the behaviour of a Laurent series at points on the bounding circles
the series (1) converges absolutely; 3) as for power series, the behaviour of a Laurent series at points on the bounding circles 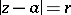 and
and 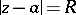 can be very diverse; 4) on any compact set
can be very diverse; 4) on any compact set 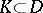 the series (1) converges uniformly; 5) the sum of the series (1) in
the series (1) converges uniformly; 5) the sum of the series (1) in 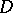 is an analytic function
is an analytic function 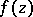 ; 6) the series (1) can be differentiated and integrated in
; 6) the series (1) can be differentiated and integrated in 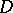 term-by-term; 7) the coefficients
term-by-term; 7) the coefficients 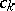 of a Laurent series are defined in terms of its sum
of a Laurent series are defined in terms of its sum 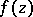 by the formulas
by the formulas
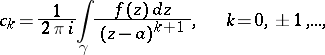 | (2) |
where 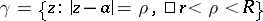 is any circle with centre
is any circle with centre  situated in
situated in 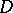 ; and 8) expansion in a Laurent series is unique, that is, if
; and 8) expansion in a Laurent series is unique, that is, if 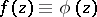 in
in 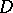 , then all the coefficients of their Laurent series in powers of
, then all the coefficients of their Laurent series in powers of 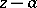 coincide.
coincide.
For the case of a centre at the point at infinity, 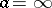 , the Laurent series takes the form
, the Laurent series takes the form
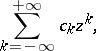 | (3) |
and now the regular part is
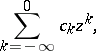 |
while the principal part is
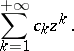 |
The domain of convergence of (3) has the form
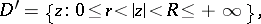 |
and formulas (2) go into
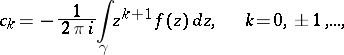 |
where 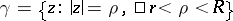 . Otherwise all the properties are the same as in the case of a finite centre
. Otherwise all the properties are the same as in the case of a finite centre  .
.
The application of Laurent series is based mainly on Laurent's theorem (1843): Any single-valued analytic function 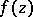 in an annulus
in an annulus 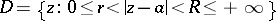 can be represented in
can be represented in 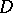 by a convergent Laurent series (1). In particular, in a punctured neighbourhood
by a convergent Laurent series (1). In particular, in a punctured neighbourhood 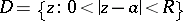 of an isolated singular point
of an isolated singular point  of single-valued character an analytic function
of single-valued character an analytic function 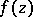 can be represented by a Laurent series, which serves as the main instrument for investigating its behaviour in a neighbourhood of an isolated singular point.
can be represented by a Laurent series, which serves as the main instrument for investigating its behaviour in a neighbourhood of an isolated singular point.
For holomorphic functions 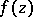 of several complex variables
of several complex variables 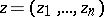 the following proposition can be regarded as the analogue of Laurent's theorem: Any function
the following proposition can be regarded as the analogue of Laurent's theorem: Any function 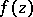 , holomorphic in the product
, holomorphic in the product 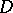 of annuli
of annuli 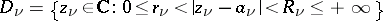 , can be represented in
, can be represented in 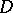 as a convergent multiple Laurent series
as a convergent multiple Laurent series
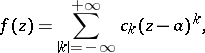 | (4) |
is which the summation extends over all integral multi-indices
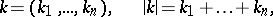 |
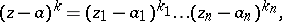 |
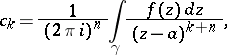 |
where 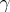 is the product of the circles
is the product of the circles 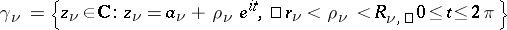 ,
, 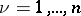 . The domain of convergence of the series (4) is logarithmically convex and is a relatively-complete Reinhardt domain. However, the use of multiple Laurent series (4) is limited, since for
. The domain of convergence of the series (4) is logarithmically convex and is a relatively-complete Reinhardt domain. However, the use of multiple Laurent series (4) is limited, since for 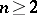 holomorphic functions
holomorphic functions 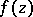 cannot have isolated singularities.
cannot have isolated singularities.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) pp. Chapt. 4 (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) pp. Vol. 1, Chapt. 2; Vol. 2, Chapt. 1 (In Russian) |
Comments
Let 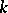 be any field. The term Laurent series is also often used to denote a formal expansion of the form
be any field. The term Laurent series is also often used to denote a formal expansion of the form
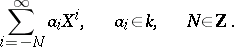 |
The expressions are added termwise and multiplied as follows:
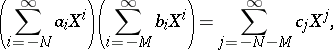 |
where
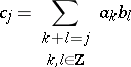 |
(note that this sum is finite). The result is a field, denoted by 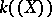 . It is the quotient field of the ring of formal power series
. It is the quotient field of the ring of formal power series 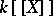 , and is called the field of formal Laurent series. A valuation is defined by
, and is called the field of formal Laurent series. A valuation is defined by 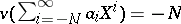 if
if 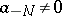 . This makes
. This makes 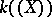 a discretely valued complete field; the ring of integers is
a discretely valued complete field; the ring of integers is 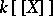 , the maximal ideal is
, the maximal ideal is 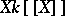 and the residue field is
and the residue field is 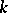 . (Cf. also Valuation.)
. (Cf. also Valuation.)
A Laurent polynomial over 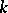 is an expression
is an expression 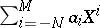 ,
, 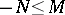 ,
, 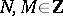 .
.
More generally one also defines (formal) Laurent series in several variables and non-commutative Laurent series, cf. [a1].
References
| [a1] | H.C. Hutchins, "Examples of commutative rings" , Polygonal (1981) |
| [a2] | P.M. Cohn, "Skew field constructions" , Cambridge Univ. Press (1977) |
| [a3] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. 241 |
| [a4] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) |
| [a5] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979) |
Laurent series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laurent_series&oldid=17288