Von Neumann algebra
A subalgebra 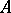 of the algebra
of the algebra  of bounded linear operators on a Hilbert space
of bounded linear operators on a Hilbert space 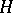 that is self-adjoint (that is, contains together with every operator
that is self-adjoint (that is, contains together with every operator 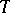 its adjoint operator
its adjoint operator 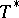 ) and that coincides with its bicommutant (that is, it contains all operators
) and that coincides with its bicommutant (that is, it contains all operators 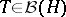 that commute with every operator commuting with all operators in
that commute with every operator commuting with all operators in 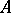 ). These algebras were introduced by J. von Neumann . According to a theorem of von Neumann, a self-adjoint subalgebra
). These algebras were introduced by J. von Neumann . According to a theorem of von Neumann, a self-adjoint subalgebra 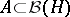 is a von Neumann algebra if and only if
is a von Neumann algebra if and only if 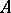 (or its unit ball) is closed in the weak, strong, ultraweak, or ultrastrong operator topology (the uniform operator topology does not suffice). A given symmetric Banach algebra
(or its unit ball) is closed in the weak, strong, ultraweak, or ultrastrong operator topology (the uniform operator topology does not suffice). A given symmetric Banach algebra 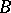 (cf. also Symmetric algebra) is isometrically isomorphic to some von Neumann algebra if and only if it is a
(cf. also Symmetric algebra) is isometrically isomorphic to some von Neumann algebra if and only if it is a 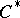 -algebra isometric to some dual space; the Banach space
-algebra isometric to some dual space; the Banach space 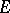 for which
for which 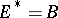 is uniquely determined up to an isometric isomorphism and can be identified with the space of ultraweakly-continuous linear forms on the von Neumann algebra isometrically isometric to
is uniquely determined up to an isometric isomorphism and can be identified with the space of ultraweakly-continuous linear forms on the von Neumann algebra isometrically isometric to 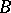 ; this space is denoted by
; this space is denoted by 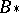 and is called the pre-dual of
and is called the pre-dual of 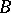 . Such symmetric Banach algebras are called
. Such symmetric Banach algebras are called 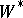 -algebras. Let
-algebras. Let 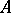 be a von Neumann algebra on a Hilbert space
be a von Neumann algebra on a Hilbert space 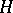 ,
, 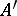 its commutator,
its commutator, 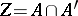 its centre,
its centre, 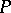 a projection belonging to
a projection belonging to 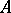 , and
, and 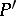 a projection belonging to
a projection belonging to 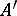 . The subspace
. The subspace 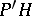 is invariant under
is invariant under 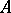 , and the family of operators from
, and the family of operators from  restricted to
restricted to 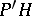 forms a von Neumann algebra in
forms a von Neumann algebra in 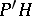 , which is denoted by
, which is denoted by 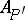 and is called the induced algebra, while the mapping
and is called the induced algebra, while the mapping  is called the induced mapping of
is called the induced mapping of 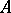 onto
onto 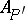 ; the family of bounded operators of the form
; the family of bounded operators of the form 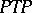 ,
, 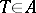 , on the subspace
, on the subspace 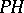 forms a von Neumann algebra
forms a von Neumann algebra 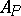 in
in 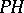 , which is called reduced. If
, which is called reduced. If 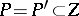 , then the reduced and the induced von Neumann algebras are the same. An isometric isomorphism of a von Neumann algebra is said to be algebraic; a von Neumann algebra on a Hilbert space
, then the reduced and the induced von Neumann algebras are the same. An isometric isomorphism of a von Neumann algebra is said to be algebraic; a von Neumann algebra on a Hilbert space 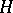 is said to be spatially isomorphic to a von Neumann algebra
is said to be spatially isomorphic to a von Neumann algebra  on a space
on a space 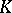 if there exists a unitary operator
if there exists a unitary operator 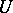 mapping
mapping 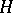 onto
onto 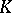 and such that
and such that 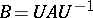 . The intersection of any family of von Neumann algebras on a given Hilbert space is a von Neumann algebra; the smallest von Neumann algebra containing a given set
. The intersection of any family of von Neumann algebras on a given Hilbert space is a von Neumann algebra; the smallest von Neumann algebra containing a given set 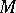 is said to be the von Neumann algebra generated by the set
is said to be the von Neumann algebra generated by the set 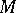 . Let
. Let 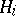 ,
, 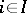 , be Hilbert spaces,
, be Hilbert spaces, 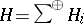 their direct sum,
their direct sum, 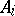 a von Neumann algebra on
a von Neumann algebra on 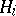 , and
, and 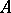 the von Neumann algebra on
the von Neumann algebra on 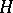 generated by those operators
generated by those operators 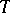 in
in 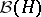 for which every
for which every  is invariant under
is invariant under 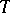 and the restriction of
and the restriction of 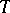 to
to 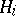 lies in
lies in 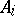 ; this von Neumann algebra is called the direct product of the
; this von Neumann algebra is called the direct product of the  and is denoted by
and is denoted by 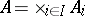 . The operations of forming the tensor product, both finite and infinite, are also defined for von Neumann algebras. A von Neumann algebra is called a factor if its centre consists of multiples of the identity.
. The operations of forming the tensor product, both finite and infinite, are also defined for von Neumann algebras. A von Neumann algebra is called a factor if its centre consists of multiples of the identity.
Let 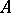 be a von Neumann algebra and
be a von Neumann algebra and 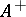 the set of its positive operators. A weight on
the set of its positive operators. A weight on 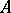 is an additive mapping
is an additive mapping 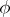 from
from 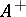 into
into 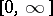 that is homogeneous under multiplication by positive numbers. A weight
that is homogeneous under multiplication by positive numbers. A weight 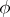 is called a trace if
is called a trace if 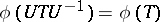 for all
for all 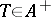 and all unitary operators
and all unitary operators 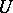 in
in 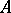 . A trace is said to be finite if
. A trace is said to be finite if 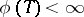 for all
for all 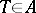 ; semi-finite if for any
; semi-finite if for any 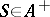 the quantity
the quantity 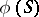 is the least upper bound of the numbers of the form
is the least upper bound of the numbers of the form 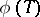 , where
, where 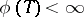 and
and 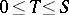 ; exact if
; exact if 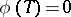 ,
, 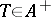 , implies
, implies 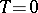 ; normal if for any increasing family
; normal if for any increasing family 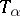 of elements in
of elements in 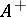 with least upper bound
with least upper bound 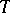 the quantity
the quantity  is the least upper bound of the numbers
is the least upper bound of the numbers 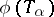 . A von Neumann algebra
. A von Neumann algebra 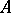 is called finite if there is a family of normal finite traces on
is called finite if there is a family of normal finite traces on 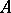 separating the points of
separating the points of 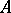 ; properly infinite if there are no non-zero finite traces on
; properly infinite if there are no non-zero finite traces on 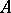 ; semi-finite if there is an exact normal semi-finite trace on
; semi-finite if there is an exact normal semi-finite trace on 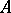 ; and purely infinite, or an algebra of type
; and purely infinite, or an algebra of type  , if there are no non-zero normal semi-finite traces on
, if there are no non-zero normal semi-finite traces on 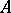 . A von Neumann algebra is called discrete, or of type
. A von Neumann algebra is called discrete, or of type 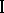 , if it is algebraically isomorphic to a von Neumann algebra with a commutative commutant; such an algebra is semi-finite. A von Neumann algebra is called continuous if for any non-zero central projection
, if it is algebraically isomorphic to a von Neumann algebra with a commutative commutant; such an algebra is semi-finite. A von Neumann algebra is called continuous if for any non-zero central projection 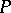 the von Neumann algebra
the von Neumann algebra 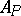 is not discrete. A continuous semi-finite algebra is said to be of type
is not discrete. A continuous semi-finite algebra is said to be of type  . A finite algebra of type
. A finite algebra of type 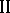 is said to be of type
is said to be of type 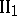 ; a properly infinite algebra of type
; a properly infinite algebra of type 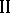 is said to be of type
is said to be of type 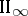 . Whether a von Neumann algebra belongs to a definite type is equivalent to the fact that its commutant belongs to the same type, but the commutant of a finite von Neumann algebra need not be a finite von Neumann algebra.
. Whether a von Neumann algebra belongs to a definite type is equivalent to the fact that its commutant belongs to the same type, but the commutant of a finite von Neumann algebra need not be a finite von Neumann algebra.
Let  be a von Neumann algebra,
be a von Neumann algebra, 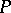 and
and  projections belonging to
projections belonging to  . Then
. Then 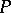 and
and 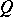 are called equivalent,
are called equivalent, 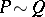 , if there is an element
, if there is an element 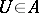 such that
such that 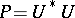 and
and 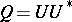 . One writes
. One writes 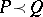 if there is a projection
if there is a projection 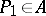 such that
such that 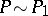 and
and 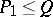 ; the relation
; the relation 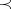 is a partial order. A classification of von Neumann algebras according to type can be carried out in terms of this relation; in particular: A projection
is a partial order. A classification of von Neumann algebras according to type can be carried out in terms of this relation; in particular: A projection 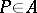 is called finite if
is called finite if 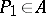 ,
, 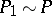 ,
, 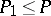 implies
implies 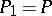 ; a von Neumann algebra is finite if and only if the identity projection is finite, and semi-finite if and only if the least upper bound of the family of finite projections is the identity projection.
; a von Neumann algebra is finite if and only if the identity projection is finite, and semi-finite if and only if the least upper bound of the family of finite projections is the identity projection.
A von Neumann algebra 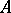 is semi-finite if and only if it can be realized as the left von Neumann algebra of a certain Hilbert algebra; the elements of the latter are those
is semi-finite if and only if it can be realized as the left von Neumann algebra of a certain Hilbert algebra; the elements of the latter are those 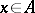 for which
for which 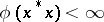 , where
, where 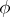 is an exact normal semi-finite trace on
is an exact normal semi-finite trace on 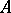 . For algebras of type
. For algebras of type  the corresponding realization can be obtained by means of generalized Hilbert algebras and weights on von Neumann algebras.
the corresponding realization can be obtained by means of generalized Hilbert algebras and weights on von Neumann algebras.
Let 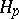 be fixed Hilbert spaces of dimension
be fixed Hilbert spaces of dimension 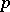 ,
, 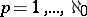 , let
, let 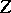 be a Borel space, let
be a Borel space, let 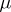 be a positive measure on
be a positive measure on 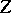 , let
, let 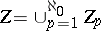 be a partition of
be a partition of 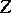 into disjoint measurable subsets, let
into disjoint measurable subsets, let 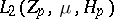 be the Hilbert space of square-summable
be the Hilbert space of square-summable 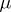 -measurable mappings of
-measurable mappings of 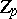 into
into 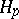 , let
, let
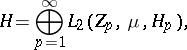 |
and let 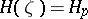 for
for 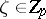 . If
. If 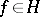 , then
, then 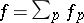 , where
, where 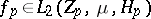 . Let
. Let 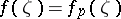 for
for 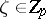 . A mapping
. A mapping 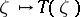 , where
, where 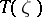 is a continuous linear operator on the Hilbert space
is a continuous linear operator on the Hilbert space 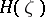 , is called a measurable field of operators if for any
, is called a measurable field of operators if for any 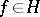 the function
the function 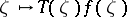 is measurable on every set
is measurable on every set 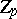 . If
. If 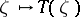 is a measurable field of operators and the function
is a measurable field of operators and the function 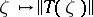 is essentially bounded on
is essentially bounded on 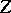 , then for every
, then for every 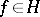 there is a unit vector
there is a unit vector 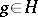 such that
such that 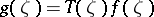
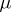 -almost everywhere. The mapping
-almost everywhere. The mapping 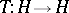 defined by
defined by 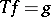 for all
for all 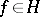 is a bounded linear operator on
is a bounded linear operator on 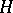 , and
, and
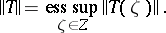 |
Such an operator 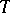 on
on 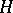 is called decomposable. Suppose that for any
is called decomposable. Suppose that for any 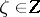 a von Neumann algebra
a von Neumann algebra 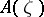 is defined on
is defined on 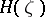 ; the mapping
; the mapping 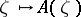 is called a measurable field of von Neumann algebras if there exists a sequence
is called a measurable field of von Neumann algebras if there exists a sequence 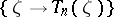 of measurable fields of operators such that for any
of measurable fields of operators such that for any 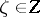 the von Neumann algebra
the von Neumann algebra 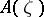 is generated by the operators
is generated by the operators 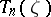 . The set of all decomposable operators
. The set of all decomposable operators 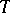 on
on 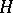 such that
such that 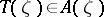 for every
for every 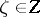 is a von Neumann algebra in
is a von Neumann algebra in 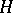 . It is denoted by
. It is denoted by
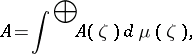 |
and is called the direct integral of the von Neumann algebras 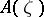 over
over 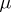 . Every von Neumann algebra on a separable Hilbert space is isomorphic to a direct integral of factors. An arbitrary von Neumann algebra has an algebraic decomposition, and this is why the theory of factors is of interest for the general theory of von Neumann algebras.
. Every von Neumann algebra on a separable Hilbert space is isomorphic to a direct integral of factors. An arbitrary von Neumann algebra has an algebraic decomposition, and this is why the theory of factors is of interest for the general theory of von Neumann algebras.
Von Neumann algebras arise naturally in problems connected with operators on a Hilbert space and have numerous applications in operator theory itself and in the representation theory of groups and algebras, as well as in the theory of dynamical systems, statistical physics and quantum field theory.
References
| [1a] | F.J. Murray, J. von Neumann, "On rings of operators" Ann. of Math. (2) , 37 (1936) pp. 116–229 |
| [1b] | F.J. Murray, J. von Neumann, "On rings of operators II" Trans. Amer. Math. Soc. , 41 (1937) pp. 208–248 |
| [2] | F.J. Murray, J. von Neumann, "On rings of operators IV" Ann. of Math. (2) , 44 (1943) pp. 716–808 |
| [3] | J. Dixmier, "Les algèbres d'opérateurs dans l'espace hilbertien: algèbres de von Neumann" , Gauthier-Villars (1957) |
| [4] | J. Dixmier, " algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [5] | S. Sakai, "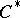 -algebras and -algebras and 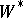 -algebras" , Springer (1971) -algebras" , Springer (1971) |
| [6a] | J. von Neumann, "On infinite direct products" Compos. Math. , 6 (1938) pp. 1–77 |
| [6b] | J. von Neumann, "On rings of operators III" Ann. of Math. (2) , 41 (1940) pp. 94–161 |
| [7] | A. Guichardet, "Produits tensoriels infinis et réprésentations des rélations d'anticommutation" Ann. Sci. Ecole Norm. Sup. , 83 (1966) pp. 1–52 |
| [8] | M. Takesaki, "Tomita's theory of modular Hilbert algebras and its applications" , Lect. notes in math. , 128 , Springer (1970) |
| [9] | L. Zsidó, "Topological decompositions of operator algebras" A. Salam (ed.) , Global analysis and its applications (Trieste, 1972) , 3 , IAEA (1974) pp. 305–308 |
| [10] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
Comments
In terms of the majorization relation 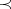 , defined above, the types of von Neumann algebras are as follows. A von Neumann algebra
, defined above, the types of von Neumann algebras are as follows. A von Neumann algebra 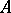 is of type
is of type 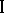 if every non-zero central projection in
if every non-zero central projection in 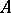 majorizes a non-zero Abelian projection. (An Abelian projection is a projection
majorizes a non-zero Abelian projection. (An Abelian projection is a projection  such that
such that 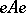 is Abelian.) If there are no non-zero finite projections in
is Abelian.) If there are no non-zero finite projections in 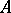 , i.e.
, i.e. 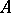 is purely infinite, then it is of type
is purely infinite, then it is of type  . If
. If 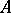 has no non-zero Abelian projections and if every non-zero central projection in
has no non-zero Abelian projections and if every non-zero central projection in 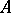 majorizes a non-zero finite projection of
majorizes a non-zero finite projection of 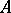 , then
, then  is of type
is of type 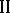 . If
. If 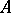 is finite and of type
is finite and of type 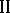 , then it is of type
, then it is of type 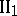 . If
. If 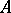 is of type
is of type 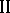 and has no non-zero central finite projections, then
and has no non-zero central finite projections, then 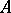 is of type
is of type 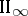 . Every von Neumann algebra is uniquely decomposable into the direct sum of von Neumann algebras of types
. Every von Neumann algebra is uniquely decomposable into the direct sum of von Neumann algebras of types 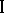 ,
, 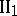 ,
, 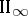 ,
,  , and a factor is hence of one of these types.
, and a factor is hence of one of these types.
A factor of type 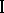 is isomorphic to
is isomorphic to 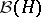 for some Hilbert space
for some Hilbert space 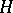 . A factor of type
. A factor of type 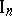 is the algebra of
is the algebra of 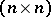 -matrices over
-matrices over 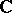 .
.
A von Neumann algebra or factor is hyperfinite if it is generated by an ascending sequence of finite factors, i.e. matrix algebras. There is just one hyperfinite type 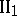 factor and one hyperfinite
factor and one hyperfinite 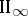 factor (up to isomorphism), [a7]. For more details on types and factors, e.g. types
factor (up to isomorphism), [a7]. For more details on types and factors, e.g. types 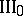 ,
, 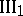 ,
, 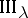 and finer classification results, cf. [a1], [a4], [a5], [a7]–[a9].
and finer classification results, cf. [a1], [a4], [a5], [a7]–[a9].
Part of a recent breakthrough in knot theory came from work on the classification of subfactors; cf. (the editorial comments to) Knot theory and references given there, as well as [a3], [a6].
References
| [a1] | O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , I-II , Springer (1979) |
| [a2] | R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , 1–2 , Acad. Press (1986) |
| [a3] | V.F.R. Jones, "A new knot polynomial and von Neumann algebras" Notices Amer. Math. Soc. , 33 (1986) pp. 219–225 |
| [a4] | V.F.R. Jones, "Subfactors and related topics" D.E. Evans (ed.) M. Takesaki (ed.) , Operator Algebras and Appl. , 2 , Cambridge Univ. Press (1988) pp. 103–118 |
| [a5] | A. Ocneanu, "Quantized groups, strong algebras, and Galois theory for algebras" D.E. Evans (ed.) M. Takesaki (ed.) , Operator Algebras and Appl. , 2 , Cambridge Univ. Press (1988) pp. 119–172 |
| [a6] | P. de la Harpe, M. Kervaire, C. Weber, "On the Jones polynomial" Enseignement Math. , 32 (1986) pp. 271–335 |
| [a7] | A. Connes, "Classification of injective factors" Ann. of Math. , 104 (1976) pp. 73–115 |
| [a8] | A. Connes, M. Takesaki, "The flow of weights on factors on type III" Tohoku Math. J. , 29 (1977) pp. 473–573 |
| [a9] | A. Connes, "Une classification des facteurs de type III" Ann. Sci. École Norm. Sup. , 6 (1973) pp. 133–252 |
Von Neumann algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Von_Neumann_algebra&oldid=17282