Group completion theorem
From Encyclopedia of Mathematics
in algebraic topology
Let 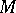 be a topological monoid and
be a topological monoid and 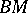 its classifying space. Let
its classifying space. Let 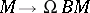 be the canonical mapping. Then
be the canonical mapping. Then 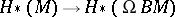 induces an isomorphism
induces an isomorphism
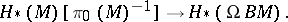 |
This theorem plays an important role in 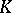 -theory.
-theory.
References
| [a1] | D. McDuff, G. Segal, "Homology fibrations and the "group completion" theorem" Invent. Math. , 31 (1976) pp. 279–287 |
| [a2] | J.F. Jardine, "The homotopical foundations of algebraic 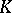 -theory" , Algebraic -theory" , Algebraic 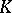 -Theory and Algebraic Number Theory , Contemp. Math. , 83 , Amer. Math. Soc. (1989) pp. 57–82 -Theory and Algebraic Number Theory , Contemp. Math. , 83 , Amer. Math. Soc. (1989) pp. 57–82 |
| [a3] | J.P. May, "Classifying spaces and fibrations" , Memoirs , 155 , Amer. Math. Soc. (1975) |
| [a4] | M.B. Barrat, S.B. Priddy, "On the homology of non-connected monoids and their associated groups" Comm. Math. Helvetici , 47 (1972) pp. 1–14 |
| [a5] | I. Moerdijk, "Bisimplicial sets and the group-completion theorem" , Algebraic 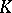 -Theory: Connections with Geometry and Topology , Kluwer Acad. Publ. (1989) pp. 225–240 -Theory: Connections with Geometry and Topology , Kluwer Acad. Publ. (1989) pp. 225–240 |
How to Cite This Entry:
Group completion theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Group_completion_theorem&oldid=17276
Group completion theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Group_completion_theorem&oldid=17276
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article