Postnikov system
natural system, homotopic resolution,  -decomposition of general type
-decomposition of general type
A sequence of fibrations
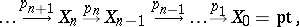 |
whose fibres are the Eilenberg–MacLane spaces 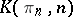 (cf. Eilenberg–MacLane space), where
(cf. Eilenberg–MacLane space), where 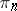 is some group (Abelian for
is some group (Abelian for 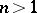 ). This system was introduced by M.M. Postnikov [1]. The space
). This system was introduced by M.M. Postnikov [1]. The space  is called the
is called the  -th term (or the
-th term (or the  -th layer) of the Postnikov system
-th layer) of the Postnikov system 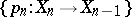 . The Postnikov system
. The Postnikov system 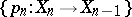 is said to converge to a space
is said to converge to a space 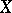 if its inverse limit
if its inverse limit 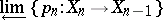 is weakly homotopy equivalent to
is weakly homotopy equivalent to 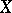 . In this case
. In this case  is called the limit of the Postnikov system
is called the limit of the Postnikov system 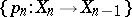 .
.
A morphism of a Postnikov system 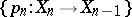 into a Postnikov system
into a Postnikov system  is a sequence of continuous mappings
is a sequence of continuous mappings  such that the diagram below is homotopy commutative. A morphism
such that the diagram below is homotopy commutative. A morphism  induces a mapping
induces a mapping  :
: 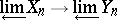 , which is called its limit.
, which is called its limit.
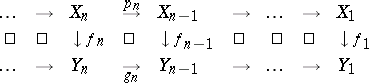 |
The definition of a Postnikov system implies that for any  the mapping
the mapping 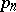 is an
is an 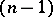 -equivalence (see Homotopy type). In particular,
-equivalence (see Homotopy type). In particular,  for
for 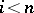 ,
, 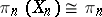 and
and 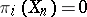 for
for 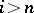 . The spaces
. The spaces 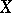 and
and 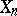 are of the same
are of the same 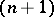 -type. In particular, if the Postnikov system is finite, i.e. if for some number
-type. In particular, if the Postnikov system is finite, i.e. if for some number 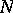 for all
for all 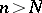 the group
the group 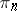 is trivial, then
is trivial, then  and
and 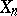 are homotopy equivalent. In the general case, for
are homotopy equivalent. In the general case, for 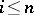 there are isomorphisms
there are isomorphisms  and
and 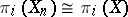 , i.e. the homology groups and the homotopy groups stabilize when
, i.e. the homology groups and the homotopy groups stabilize when  tends to infinity. For any CW-complex
tends to infinity. For any CW-complex  of dimension
of dimension 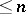 the sets
the sets 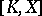 and
and 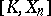 coincide. The characteristic class
coincide. The characteristic class 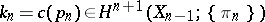 of the fibration
of the fibration 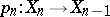 , i.e. the image under the transgression
, i.e. the image under the transgression
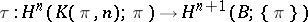 |
of the fundamental class 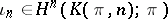 , is called the
, is called the  -th
-th 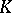 -invariant (or the
-invariant (or the  -th Postnikov factor) of the Postnikov system or of its limit
-th Postnikov factor) of the Postnikov system or of its limit 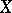 . For any
. For any  the
the  -th term of the Postnikov system, and hence the
-th term of the Postnikov system, and hence the 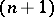 -type of
-type of 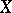 , are completely determined by the groups
, are completely determined by the groups  and the
and the 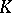 -invariants
-invariants 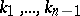 . Often the double sequence below is called a Postnikov system:
. Often the double sequence below is called a Postnikov system:
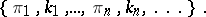 |
A space  is the limit of a Postnikov system
is the limit of a Postnikov system 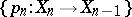 if and only if there exist
if and only if there exist  -equivalences
-equivalences  such that
such that 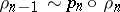 for any
for any  . Limits of morphisms of a Postnikov system are characterized analogously.
. Limits of morphisms of a Postnikov system are characterized analogously.
There exists a version of the notion of a Postnikov system which sometimes turns out to be more useful. In this version the spaces 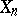 are assumed to be CW-complexes such that
are assumed to be CW-complexes such that 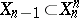 and
and 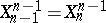 , and the mappings
, and the mappings 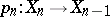 are taken to be cellular mappings (which are not fibrations any more) such that, first,
are taken to be cellular mappings (which are not fibrations any more) such that, first, 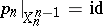 and, secondly, the homotopy fibre of the mapping
and, secondly, the homotopy fibre of the mapping  (i.e. the fibre of this mapping turned into a fibration) is the space
(i.e. the fibre of this mapping turned into a fibration) is the space 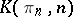 . Such Postnikov systems are called cellular. The limit of a cellular Postnikov system is a CW-complex
. Such Postnikov systems are called cellular. The limit of a cellular Postnikov system is a CW-complex 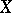 for which
for which 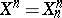 for any
for any 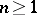 . An arbitrary Postnikov system is homotopy equivalent to a cellular Postnikov system.
. An arbitrary Postnikov system is homotopy equivalent to a cellular Postnikov system.
The fundamental theorem in the theory of Postnikov systems states (see [1], [6]) that each space 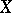 is the limit of some unique (up to isomorphism) Postnikov system
is the limit of some unique (up to isomorphism) Postnikov system 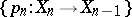 . This Postnikov system is called the Postnikov system of the space
. This Postnikov system is called the Postnikov system of the space 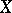 . A version of the fundamental theorem for mappings holds: Any mapping
. A version of the fundamental theorem for mappings holds: Any mapping  is the limit of some morphism
is the limit of some morphism 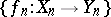 of the Postnikov system
of the Postnikov system 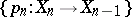 of
of 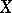 into the Postnikov system
into the Postnikov system 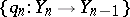 of
of 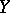 . This morphism is called the Postnikov system of the mapping
. This morphism is called the Postnikov system of the mapping 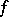 (it is also called the homotopic resolution, the
(it is also called the homotopic resolution, the 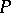 -system of general type or the Moore–Postnikov system of the mapping). For a constant mapping
-system of general type or the Moore–Postnikov system of the mapping). For a constant mapping 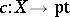 of a path-connected space
of a path-connected space 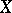 its Postnikov system coincides with the Postnikov system of the space
its Postnikov system coincides with the Postnikov system of the space 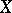 .
.
In applications the so-called standard Postnikov systems (often called just Postnikov systems) are widely spread. These systems are Postnikov systems which consist of the principal fibrations  induced from the standard Serre fibrations
induced from the standard Serre fibrations 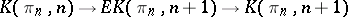 by the Postnikov factors
by the Postnikov factors  interpreted as mappings
interpreted as mappings 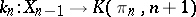 by virtue of the representation of the cohomology group as
by virtue of the representation of the cohomology group as 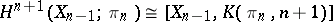 . All spaces which are homotopy simple in all dimensions (Abelian spaces in the terminology of [2]) and only these spaces have standard Postnikov systems (see [3], [4]).
. All spaces which are homotopy simple in all dimensions (Abelian spaces in the terminology of [2]) and only these spaces have standard Postnikov systems (see [3], [4]).
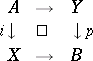
Standard Postnikov systems are applied to solve extension and lifting problems to which numerous problems in algebraic topology are reduced. The combined formulation of these problems is the following. Let a (homotopy) commutative square of spaces and mappings be given in which the mapping 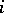 is a closed cofibration with cofibre
is a closed cofibration with cofibre  and
and  is a fibration with fibre
is a fibration with fibre 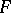 . The question is whether there exists a mapping
. The question is whether there exists a mapping  such that both triangles obtained are (homotopy) commutative.
such that both triangles obtained are (homotopy) commutative.
 |
Further, if such a mapping does exist, then one is expected to determine the set 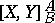 of homotopy classes of mappings
of homotopy classes of mappings  "below A" (i.e.
"below A" (i.e. 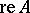 ) and "above B" . Suppose that for the fibration
) and "above B" . Suppose that for the fibration 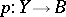 there exists a standard Postnikov system
there exists a standard Postnikov system 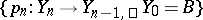 (for this purpose, for example, it is sufficient for the spaces
(for this purpose, for example, it is sufficient for the spaces 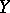 and
and 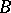 to be simply connected). The problem of relative lifting is solved step by step.
to be simply connected). The problem of relative lifting is solved step by step.
Consider the "elementary" problem of the relative lifting of a mapping  from the
from the 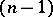 -st term of the Postnikov system to its
-st term of the Postnikov system to its  -th term:
-th term:
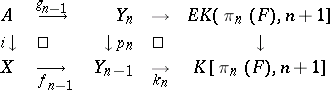 |
The mappings 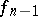 and
and  define a mapping
define a mapping 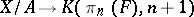 , i.e. a cohomology class
, i.e. a cohomology class 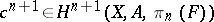 , called an obstruction. The mapping
, called an obstruction. The mapping  can be lifted to
can be lifted to 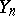 if and only if
if and only if 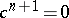 . Two liftings
. Two liftings  and
and 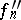 determine an element
determine an element 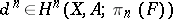 , called a difference, which is equal to zero if and only if the liftings
, called a difference, which is equal to zero if and only if the liftings 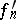 and
and  are homotopic.
are homotopic.
Thus, the problem of relative lifting is solved if the sequentially occurring obstructions 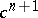 vanish (for example, if
vanish (for example, if 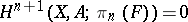 ). A lifting is unique if the sequentially occurring differences
). A lifting is unique if the sequentially occurring differences  vanish (for example, if
vanish (for example, if  ). In the case when the cofibration is an imbedding of CW-complexes, the obstruction
). In the case when the cofibration is an imbedding of CW-complexes, the obstruction  and the difference
and the difference 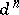 coincide with usual "cell-wise" obstruction and difference (cf. Difference cochain and chain).
coincide with usual "cell-wise" obstruction and difference (cf. Difference cochain and chain).
For simply-connected spaces 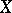 with finitely-generated homology groups the Postnikov system is effectively computable [5] and, hence, the homotopy type of
with finitely-generated homology groups the Postnikov system is effectively computable [5] and, hence, the homotopy type of  is effectively computable as well. However, in practice, for the majority of spaces one succeeds to compute only initial segments of Postnikov systems, which is due to the sharply increasing complexity of the computations. For computations one uses the method of cohomology operations (cf. Cohomology operation).
is effectively computable as well. However, in practice, for the majority of spaces one succeeds to compute only initial segments of Postnikov systems, which is due to the sharply increasing complexity of the computations. For computations one uses the method of cohomology operations (cf. Cohomology operation).
The dual of the Postnikov system is the Cartan–Serre system
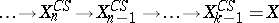 |
of a space 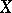 , consisting of fibrations whose fibres are the Eilenberg–MacLane spaces
, consisting of fibrations whose fibres are the Eilenberg–MacLane spaces  . The space
. The space  is called the (
is called the (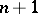 )-st killing space for
)-st killing space for  . The terms
. The terms 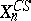 of the Cartan–Serre system are homotopy fibres of (
of the Cartan–Serre system are homotopy fibres of (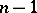 )-equivalences
)-equivalences  for the Postnikov system of
for the Postnikov system of 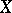 , and the terms
, and the terms  of a Postnikov system are loop spaces over the fibres of
of a Postnikov system are loop spaces over the fibres of  .
.
A split Postnikov system is a sequence of principal fibrations
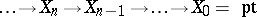 |
whose fibres are the Eilenberg–MacLane spaces 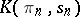 ,
,  . Split Postnikov systems are the principal tool in the studies of so-called nilpotent spaces and, in particular, of their localizations (see Localization in categories, [2], [6], [7]). There also exist other versions of Postnikov systems (see [6]).
. Split Postnikov systems are the principal tool in the studies of so-called nilpotent spaces and, in particular, of their localizations (see Localization in categories, [2], [6], [7]). There also exist other versions of Postnikov systems (see [6]).
References
| [1] | M.M. Postnikov, "Studies on the homotopy theory of continuous mappings" , 1–2 , Moscow (1955) (In Russian) |
| [2] | M.M. Postnikov, "Localization of topological spaces" Russian Math. Surveys , 32 : 6 (1977) pp. 121–184 Uspekhi Mat. Nauk , 32 : 6 (1977) pp. 117–181 |
| [3] | R.E. Mosher, M.C. Tangora, "Cohomology operations and applications in homotopy theory" , Harper & Row (1968) pp. Chapt. 13 |
| [4] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [5] | E.H. Brown, "Finite computability of Postnikov complexes" Ann. of Math. (2) , 65 (1957) pp. 1–20 |
| [6] | H.J. Baues, "Obstruction theory of homotopy classification of maps" , Springer (1977) |
| [7] | P. Hilton, G. Mislin, J. Roitberg, "Localization of nilpotent groups and spaces" , North-Holland (1975) |
Comments
References
| [a1] | G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. Chapt. IX |
| [a2] | B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. Chapt. 17 |
Postnikov system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Postnikov_system&oldid=17272