Domain
A non-empty connected open set in a topological space  . The closure
. The closure  of a domain
of a domain  is called a closed domain; the closed set
is called a closed domain; the closed set  is called the boundary of
is called the boundary of  . The points
. The points  are also called the interior points of
are also called the interior points of  ; the points
; the points  are called the boundary points of
are called the boundary points of  ; the points of the complement
; the points of the complement  are called the exterior points of
are called the exterior points of 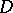 .
.
Any two points of a domain 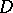 in the real Euclidean space
in the real Euclidean space 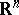 ,
,  (or in the complex space
(or in the complex space  ,
, 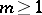 , or on a Riemann surface or in a Riemannian domain), can be joined by a path (or arc) lying completely in
, or on a Riemann surface or in a Riemannian domain), can be joined by a path (or arc) lying completely in 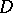 ; if
; if 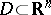 or
or  , they can even be joined by a polygonal path with a finite number of edges. Finite and infinite open intervals are the only domains in the real line
, they can even be joined by a polygonal path with a finite number of edges. Finite and infinite open intervals are the only domains in the real line  ; their boundaries consist of at most two points. A domain
; their boundaries consist of at most two points. A domain  in the plane is called simply connected if any closed path in
in the plane is called simply connected if any closed path in  can be continuously deformed to a point, remaining throughout in
can be continuously deformed to a point, remaining throughout in 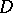 . In general, the boundary of a simply-connected domain in the (open) plane
. In general, the boundary of a simply-connected domain in the (open) plane  or
or 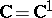 can consist of any number
can consist of any number 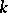 of connected components,
of connected components,  . If
. If  is regarded as a domain in the compact extended plane
is regarded as a domain in the compact extended plane 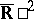 or
or  and the number
and the number  of boundary components is finite, then
of boundary components is finite, then 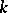 is called the connectivity order of
is called the connectivity order of 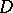 ; for
; for  ,
,  is called multiply connected. In other words, the connectivity order
is called multiply connected. In other words, the connectivity order 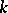 is one more than the minimum number of cross-cuts joining components of the boundary in pairs that are necessary to make
is one more than the minimum number of cross-cuts joining components of the boundary in pairs that are necessary to make 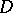 simply connected. For
simply connected. For 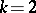 ,
,  is called doubly connected, for
is called doubly connected, for  , triply connected, etc.; for
, triply connected, etc.; for  one has finitely-connected domains and for
one has finitely-connected domains and for  infinitely-connected domains. The connectivity order of a plane domain characterizes its topological type. The topological types of domains in
infinitely-connected domains. The connectivity order of a plane domain characterizes its topological type. The topological types of domains in  ,
,  , or in
, or in  ,
,  , cannot be characterized by a single number.
, cannot be characterized by a single number.
Even for a simply-connected plane domain  the metric structure of the boundary
the metric structure of the boundary  can be very complicated (see Limit elements). In particular, the boundary points can be divided into accessible points
can be very complicated (see Limit elements). In particular, the boundary points can be divided into accessible points 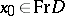 , for which there exists a path
, for which there exists a path  ,
,  ,
,  ,
, 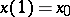 , joining
, joining  in
in  with any point
with any point  , and inaccessible points, for which no such paths exists (cf. Attainable boundary point). For any simply-connected plane domain
, and inaccessible points, for which no such paths exists (cf. Attainable boundary point). For any simply-connected plane domain 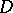 the set of accessible points of
the set of accessible points of  is everywhere dense in
is everywhere dense in  .
.
A domain 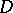 in
in  or
or 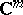 is called bounded, or finite, if
is called bounded, or finite, if
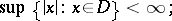 |
if not, 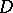 is called unbounded or infinite. A closed plane Jordan curve divides the plane
is called unbounded or infinite. A closed plane Jordan curve divides the plane 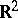 or
or 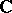 into two Jordan domains: A finite domain
into two Jordan domains: A finite domain 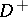 and an infinite domain
and an infinite domain 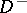 . All boundary points of a Jordan domain are accessible.
. All boundary points of a Jordan domain are accessible.
Comments
Instead of  , the boundary of
, the boundary of 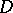 is also denoted by
is also denoted by  or
or 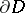 .
.
From the definition it can be seen that a domain is bounded if (and only if) it is contained in a ball centred at the coordinate origin and of finite radius.
Domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Domain&oldid=17271