Linear connection

A linear connection on a differentiable manifold is a differential-geometric structure on associated with an affine connection on . For every affine connection a parallel displacement of vectors is defined, which makes it possible to define for every curve in a linear mapping of tangent spaces . In this sense an affine connection determines a linear connection on , to which all concepts and constructions can be transferred which only depend on the displacement of vectors and, more generally, of tensors. A linear connection on is a connection in the principal bundle of frames in the tangent spaces , , and is defined in one of the following three equivalent ways:

1) by a connection object , satisfying the following transformation law on intersections of domains of local charts:

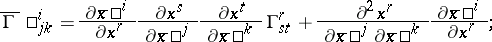2) by a matrix of 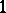-forms on the principal frame bundle , such that the -forms

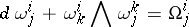in each local coordinate system can be expressed in the form

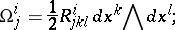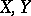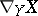3) by the bilinear operator of covariant differentiation, which associates with two vector fields on a third vector field and has the properties:

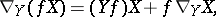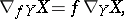where 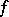is a smooth function on .

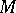Every linear connection on 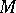uniquely determines an affine connection on 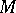canonically associated with it. It is determined by the involute of any curve in . To obtain this involute one must first define linearly independent parallel vector fields along 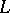, then expand the tangent vector field to in terms of them,

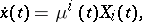and finally find in the solution 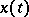of the differential equation

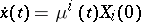with initial value . At an arbitrary point of an affine mapping of tangent affine spaces

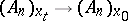is now defined by a mapping of frames

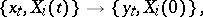where .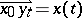

A linear connection is often identified with the affine connection canonically associated with it, by using the one-to-one correspondence between them.

A linear connection on a vector bundle is a differential-geometric structure on a differentiable vector bundle which associates with every piecewise-smooth curve in beginning at and ending at a linear isomorphism of the fibres and as vector spaces, called parallel displacement along . A linear connection is determined by a horizontal distribution on the principal bundle of frames in the fibres of the given vector bundle. Analytically, a linear connection is specified by a matrix of 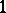-forms on 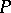, where , where 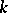denotes the dimension of the fibres, such that the -forms

are semi-basic, that is, in every local coordinate system 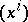on they can be expressed in the form

The horizontal distribution is determined, moreover, by the differential system on . The -forms are called curvature forms. According to the holonomy theorem they determine the holonomy group of the linear connection.

A linear connection in a fibre bundle 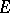is a connection under which the tangent vectors of horizontal curves beginning at a given point 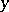of form a vector subspace 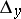of ; the linear connection is determined by the horizontal distribution : .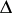

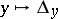References

[1]	A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French)
[2]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963)

References

[a1]	S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III