Projective determination of a metric
An introduction in subsets of a projective space, by methods of projective geometry, of a metric such that these subsets become isomorphic to a Euclidean, hyperbolic or elliptic space. This is achieved by distinguishing in the class of all projective transformations (cf. Projective transformation) those transformations that generate in these subsets a group of transformations isomorphic to the corresponding group of motions. The presence of motions allows one "to lay off" segments of a straight line from a given point in a given direction, thereby introducing the concept of the length of a segment.
To obtain the Euclidean determination of a metric in the  -dimensional projective space
-dimensional projective space 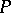 , one should distinguish in this space an
, one should distinguish in this space an 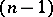 -dimensional hyperplane
-dimensional hyperplane 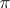 , called the ideal hyperplane, and establish in this hyperplane an elliptic polar correspondence
, called the ideal hyperplane, and establish in this hyperplane an elliptic polar correspondence 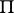 of points and
of points and 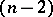 -dimensional hyperplanes (that is, a polar correspondence under which no point belongs to the
-dimensional hyperplanes (that is, a polar correspondence under which no point belongs to the 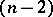 -dimensional plane corresponding to it).
-dimensional plane corresponding to it).
Suppose that 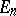 is a subset of the projective space
is a subset of the projective space 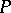 obtained by removing from it an ideal hyperplane; and let
obtained by removing from it an ideal hyperplane; and let 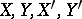 be points in
be points in 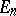 . Two segments
. Two segments 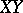 and
and 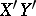 are said to be congruent if there exists a projective transformation
are said to be congruent if there exists a projective transformation 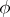 taking the points
taking the points  and
and 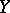 to the points
to the points 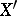 and
and 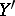 , respectively, and preserving the polarity
, respectively, and preserving the polarity 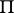 .
.
The concept of congruence of segments thus defined allows one to introduce a metric of a Euclidean space in 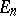 . For this, in the projective space
. For this, in the projective space 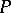 a system of projective coordinates is introduced with the basis simplex
a system of projective coordinates is introduced with the basis simplex  , where the point
, where the point 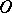 does not not belong to the ideal hyperplane
does not not belong to the ideal hyperplane 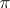 while the points
while the points 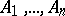 do. Suppose that the point
do. Suppose that the point 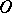 in this coordinate system has the coordinates
in this coordinate system has the coordinates 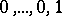 , and that the points
, and that the points 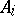 ,
, 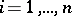 , have the coordinates
, have the coordinates
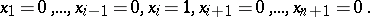 |
Then the elliptic polar correspondence 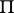 defined in the hyperplane
defined in the hyperplane 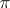 can be written in the form
can be written in the form
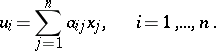 |
The matrix 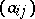 of this correspondence is symmetric, and the quadratic form
of this correspondence is symmetric, and the quadratic form
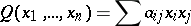 |
corresponding to it is positive definite. Let
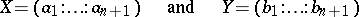 |
be two points in 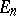 (that is,
(that is, 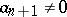 ,
, 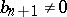 ). One may set
). One may set
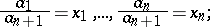 |
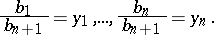 |
Then the distance 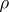 between the points
between the points 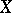 and
and 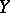 is defined by
is defined by
 |
For a projective determination of the metric of the  -dimensional hyperbolic space, in the
-dimensional hyperbolic space, in the  -dimensional projective space
-dimensional projective space 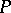 a set
a set 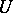 of interior points of a real oval hypersurface
of interior points of a real oval hypersurface 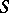 of order two is considered. Let
of order two is considered. Let 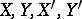 be points in
be points in 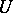 ; then the segments
; then the segments 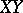 and
and  are assumed to be congruent if there is a projective transformation of the space
are assumed to be congruent if there is a projective transformation of the space 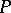 under which the hypersurface
under which the hypersurface 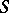 is mapped onto itself and the points
is mapped onto itself and the points 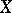 and
and 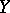 are taken to the points
are taken to the points 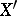 and
and 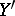 , respectively. The concept of congruence of segments thus introduced establishes in
, respectively. The concept of congruence of segments thus introduced establishes in 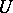 the metric of the hyperbolic space. The length of a segment in this metric is defined by
the metric of the hyperbolic space. The length of a segment in this metric is defined by
 |
where 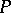 and
and 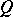 are the points of intersection of the straight line
are the points of intersection of the straight line 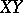 with the hypersurface
with the hypersurface 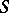 and
and  is a positive number related to the curvature of the Lobachevskii space. To introduce an elliptic metric in the projective space
is a positive number related to the curvature of the Lobachevskii space. To introduce an elliptic metric in the projective space 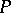 , one considers an elliptic polar correspondence
, one considers an elliptic polar correspondence 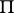 in this space. Two segments
in this space. Two segments 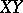 and
and 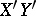 are said to be congruent if there exists a projective transformation
are said to be congruent if there exists a projective transformation 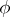 taking the points
taking the points  and
and 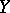 to the points
to the points 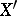 and
and 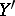 , respectively, and preserving the polar mapping
, respectively, and preserving the polar mapping 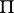 (that is, for any point
(that is, for any point 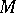 and its polar
and its polar 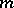 , the polar of the point
, the polar of the point  is
is 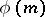 ). If the elliptic polar correspondence
). If the elliptic polar correspondence 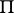 is given by the relations
is given by the relations
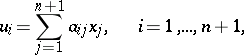 |
then the matrix 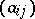 is symmetric and the quadratic form corresponding to it is positive definite. Now, if
is symmetric and the quadratic form corresponding to it is positive definite. Now, if
 |
then
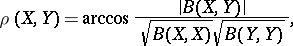 |
where 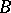 is the bilinear form given by the matrix
is the bilinear form given by the matrix 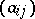 .
.
In all the cases considered (if a real projective space is completed to a complex projective space), under the projective transformations defining the congruence of segments, that is, under motions, some hypersurfaces of the second order remain invariant; these are called absolutes. In the case of a Euclidean determination of a metric, the absolute is an imaginary 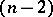 -dimensional oval surface of order two. In the case of a hyperbolic determination of a metric, the absolute is an oval
-dimensional oval surface of order two. In the case of a hyperbolic determination of a metric, the absolute is an oval 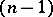 -dimensional real hypersurface of order two. In the case of an elliptic determination of a metric, the absolute is an imaginary
-dimensional real hypersurface of order two. In the case of an elliptic determination of a metric, the absolute is an imaginary 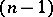 -dimensional oval hypersurface of order two.
-dimensional oval hypersurface of order two.
References
| [1] | N.V. Efimov, "Higher geometry" , MIR (1980) (Translated from Russian) |
| [2] | N.A. Glagolev, "Projective geometry" , Moscow (1963) (In Russian) |
| [3] | H. Busemann, P.J. Kelly, "Projective geometry and projective metrics" , Acad. Press (1953) |
Comments
References
| [a1] | S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972) |
Projective determination of a metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_determination_of_a_metric&oldid=17265