Maximum-entropy spectral estimator

auto-regressive spectral estimator

An estimator 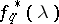for the spectral density 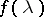of a discrete-time stationary stochastic process such that 1) the first 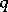values of the auto-correlations are equal to the sample auto-correlations calculated from the observational data, and 2) the entropy of the Gaussian stochastic process with spectral density 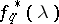is maximized subject to condition 1). If 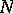sample values 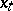, , 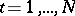are known from observing a realization of a real stationary process 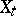having spectral density 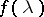, then the maximum-entropy spectral estimator 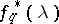is defined by the relations

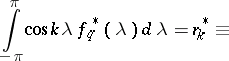(1)

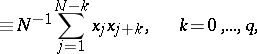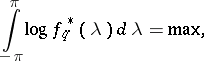(2)

where the sign denotes "equal by definition" . The maximum-entropy spectral estimator has the form

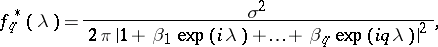(3)

where the coefficients 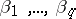and 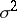are given by the 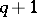equations (1) (see, e.g., [1], [9], [10]). Formula (3) shows that the maximum-entropy spectral estimator coincides with the so-called auto-regressive spectral estimator (introduced in [2], [3]). The positive integer 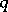here plays a role related to that played by the reciprocal width of a spectral window in the case of non-parametric estimation of the spectral density by periodogram smoothing (see Spectral window; Statistical problems in the theory of stochastic processes). There are several methods for estimating the optimal value of 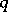from given observations (see, for example, [1], [4], [5], [8]). The values of the coefficients 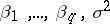can be found using a solution of the Yule–Walker equations

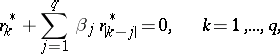(4)

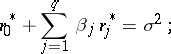(5)

there are also other, numerically more convenient, methods for calculating these coefficients (see, e.g., [1], [4]–[6], [10]).

In the case of small sample size or spectral densities of complex form, maximum-entropy spectral estimators and parametric spectral estimators (cf. Spectral estimator, parametric), which generalize them, possess definite advantages over non-parametric estimators of 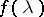: they usually have a more regular form and possess better resolving power, that is, they permit one to better distinguish close peaks of the graph of the spectral density (see [1], [4]–[7]). Therefore maximum-entropy spectral estimators are widely used in the applied spectral analysis of a stationary stochastic process.

References

[1]	D.G. Childers (ed.) , Modern spectrum analysis , IEEE (1978)
[2]	E. Parzen, "An approach to empirical time series analysis" Radio Sci. , 68 (1964) pp. 937–951
[3]	H. Akaike, "Power spectrum estimation through autoregressive model fitting" Ann. Inst. Stat. Math. , 21 : 3 (1969) pp. 407–419
[4]	S.S. Haykin (ed.) , Nonlinear methods of spectral analysis , Springer (1979)
[5]	S.M. Kay, S.L. Marpl, "Spectrum analysis—a modern perspective" Proc. IEEE , 69 : 11 (1981) pp. 1380–1419
[6]	"Spectral estimation" Proc. IEEE , 70 : 9 (1982) ((Special Issue))
[7]	V.F. Pisarenko, "Sampling properties of maximum entropy spectral estimation" , Numerical Seismology , Moscow (1977) pp. 118–149 (In Russian)
[8]	J.G. de Gooyer, B. Abraham, A. Gould, L. Robinson, "Methods for determining the order of an autoregressive-moving average process: A survey" Internat. Stat. Rev. , 55 (1985) pp. 301–329
[9]	M.B. Priestley, "Spectral analysis and time series" , 1–2 , Acad. Press (1981)
[10]	A. Papoulis, "Probability, random variables and stochastic processes" , McGraw-Hill (1984)