Parallelizable manifold
A manifold  of dimension
of dimension  admitting a (global) field of frames
admitting a (global) field of frames  (cf. also Frame), that is,
(cf. also Frame), that is,  vector fields
vector fields  that are linearly independent at each point. The field
that are linearly independent at each point. The field  determines an isomorphism of the tangent bundle
determines an isomorphism of the tangent bundle  onto the trivial bundle
onto the trivial bundle  , which sends a tangent vector
, which sends a tangent vector  to its coordinates with respect to the frame
to its coordinates with respect to the frame 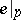 and its origin. Therefore a parallelizable manifold can also be defined as a manifold having a trivial tangent bundle. Examples of parallelizable manifolds are open submanifolds of a Euclidean space, all three-dimensional manifolds, the space of an arbitrary Lie group, and the manifolds of frames of an arbitrary manifold. The sphere
and its origin. Therefore a parallelizable manifold can also be defined as a manifold having a trivial tangent bundle. Examples of parallelizable manifolds are open submanifolds of a Euclidean space, all three-dimensional manifolds, the space of an arbitrary Lie group, and the manifolds of frames of an arbitrary manifold. The sphere  is a parallelizable manifold only for
is a parallelizable manifold only for 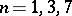 . A necessary and sufficient condition for the parallelizability of a
. A necessary and sufficient condition for the parallelizability of a 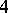 -dimensional manifold is the vanishing of the second Stiefel–Whitney characteristic class. In the general case the vanishing of the second characteristic classes of Stiefel— Whitney, Chern and Pontryagin are necessary but not sufficient conditions for a manifold to be parallelizable.
-dimensional manifold is the vanishing of the second Stiefel–Whitney characteristic class. In the general case the vanishing of the second characteristic classes of Stiefel— Whitney, Chern and Pontryagin are necessary but not sufficient conditions for a manifold to be parallelizable.
Comments
References
| [a1] | M. Gromov, "Partial differential relations" , Springer (1986) (Translated from Russian) |
| [a2] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
Parallelizable manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parallelizable_manifold&oldid=17256