Uniformizing element
From Encyclopedia of Mathematics
An element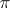 
of a discrete valuation ring 
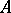(cf. Discretely-normed ring) with prime ideal 
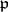such that 
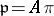. If 
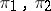are two uniformizing elements in 
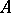, then the element 
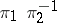is invertible in 
. Let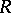 
be a system of representatives in 
for the elements of the residue field 
. Then any element 
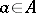can be uniquely expressed as a power series 
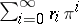, where 
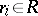and 
is a uniformizing element. If the ring 
is complete relative to the discrete valuation, then any power series of the above form represents an element 
.
If 
is the local ring of functions at a simple point 
of an algebraic curve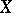 
, then 
is a uniformizing element if and only if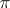 
has a zero of order one at 
.
Comments
References
| [a1] | E. Weiss, "Algebraic number theory" , McGraw-Hill (1963) pp. Sects. 4–9 |
How to Cite This Entry:
Uniformizing element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniformizing_element&oldid=17250
Uniformizing element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniformizing_element&oldid=17250
This article was adapted from an original article by L.V. Kuz'min (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article