Fubini model
A model of the manifold of lines in a three-dimensional elliptic space 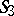 on a pair of two-dimensional elliptic planes
on a pair of two-dimensional elliptic planes 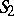 . Pairs of mutually-polar lines in
. Pairs of mutually-polar lines in 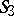 are represented in a one-to-one manner by pairs of diametrically-opposite points of two spheres of unit radius in the Euclidean space
are represented in a one-to-one manner by pairs of diametrically-opposite points of two spheres of unit radius in the Euclidean space 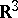 . When one identifies diametrically-opposite points, one obtains a one-to-one representation of pairs of polar lines in
. When one identifies diametrically-opposite points, one obtains a one-to-one representation of pairs of polar lines in 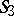 by points of two elliptic planes
by points of two elliptic planes 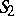 . The manifold of pairs of polar lines is homeomorphic to the topological product of these two planes
. The manifold of pairs of polar lines is homeomorphic to the topological product of these two planes 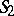 . A motion of
. A motion of 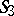 is represented in the Fubini model by independent motions of the two planes
is represented in the Fubini model by independent motions of the two planes 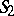 : Every connected group of motions of
: Every connected group of motions of 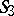 is isomorphic to the direct product of two groups of motions of
is isomorphic to the direct product of two groups of motions of 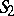 ; the group of motions of
; the group of motions of 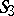 is isomorphic to the direct product of the two groups of motions of the pair of planes
is isomorphic to the direct product of the two groups of motions of the pair of planes 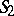 .
.
A Fubini model can also be constructed for a three-dimensional hyperbolic space 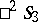 . In this case one uses the Plücker interpretation of the projective space
. In this case one uses the Plücker interpretation of the projective space 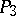 in
in 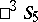 . The group of motions of
. The group of motions of 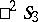 is isomorphic to the direct product of the two groups of motions of
is isomorphic to the direct product of the two groups of motions of 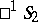 ; it is represented in the Plücker model by the subgroup of the group of motions of
; it is represented in the Plücker model by the subgroup of the group of motions of 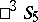 consisting of the motions that map two mutually-polar hyperbolic
consisting of the motions that map two mutually-polar hyperbolic  -planes into themselves. The lines of intersection of these planes with the absolute of
-planes into themselves. The lines of intersection of these planes with the absolute of 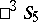 form a family of straight line generators of a ruled quadric. The manifold of pairs of polar elliptic lines in
form a family of straight line generators of a ruled quadric. The manifold of pairs of polar elliptic lines in 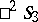 is homeomorphic to the topological product of proper domains of the two planes
is homeomorphic to the topological product of proper domains of the two planes 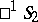 , that is, to the topological product of two discs, and the manifold of pairs of polar hyperbolic lines is homeomorphic to the product of ideal domains of the two planes
, that is, to the topological product of two discs, and the manifold of pairs of polar hyperbolic lines is homeomorphic to the product of ideal domains of the two planes 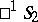 , that is, the topological product of two Möbius strips.
, that is, the topological product of two Möbius strips.
The model was proposed by G. Fubini [1].
References
| [1] | G. Fubini, Ann. Scuola Norm. Sup. Pisa , 9 (1904) pp. 1–74 |
| [2] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
Comments
The constructions of Fubini follow easily from the decomposition of the orthogonal group 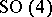 given by the quaternions: see [a1].
given by the quaternions: see [a1].
References
| [a1] | M. Berger, "Geometry" , II , Springer (1987) pp. Sect. 8.9 |
Fubini model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fubini_model&oldid=17226