Birational mapping

birational isomorphism

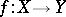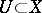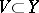A rational mapping between algebraic varieties inducing an isomorphism of their fields of rational functions. 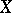In a more general setting, a rational mapping of schemes is said to be a birational mapping if it satisfies one of the following equivalent conditions: 1) there exist dense open sets and such that is defined on and realizes an isomorphism of subschemes ; 2) if , are the sets of generic points of the irreducible components of the schemes and 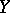respectively, 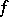induces a bijective correspondence between the sets 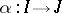and an isomorphism of local rings 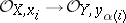for each .

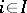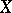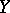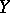If the schemes and are irreducible and reduced, the local rings of their generic points become identical with the fields of rational functions on and , respectively. In such a case the birational mapping 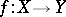induces, in accordance with condition 2), an isomorphism of the fields of rational functions: .

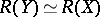Two schemes 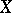and 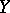are said to be birationally equivalent or birationally isomorphic if a birational mapping 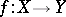exists. A birational morphism is a special case of a birational mapping.

The simplest birational mapping is a monoidal transformation with a non-singular centre. For smooth complete varieties of dimension 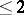any birational mapping may be represented as the composite of such transformations and their inverses. At the time of writing (1986) this question remains open in the general case.

References

[1]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)
[2]	R. Hartshorne, "Algebraic geometry" , Springer (1977)