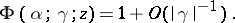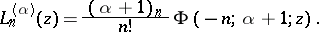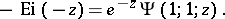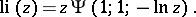Kummer function, Pochhammer function
A solution of the confluent hypergeometric equation
 | (1) |
The function may be defined using the so-called Kummer series
 | (2) |
where 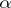 and
and 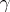 are parameters which assume any real or complex values except for
are parameters which assume any real or complex values except for  and
and  is a complex variable. The function
is a complex variable. The function 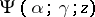 is called the confluent hypergeometric function of the first kind. The second linearly independent solution of equation (1),
is called the confluent hypergeometric function of the first kind. The second linearly independent solution of equation (1),
is called the confluent hypergeometric function of the second kind.
The confluent hypergeometric function  is an entire analytic function in the entire complex
is an entire analytic function in the entire complex  -plane; if
-plane; if  is fixed, it is an entire function of
is fixed, it is an entire function of 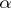 and a meromorphic function of
and a meromorphic function of 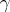 with simple poles at the points
with simple poles at the points  . The confluent hypergeometric function
. The confluent hypergeometric function 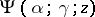 is an analytic function in the complex
is an analytic function in the complex  -plane with the slit
-plane with the slit 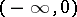 and an entire function of
and an entire function of 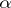 and
and 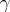 .
.
The confluent hypergeometric function  is connected with the hypergeometric function
is connected with the hypergeometric function  by the relation
by the relation
Elementary relationships. The four functions 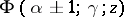 ,
,  are called adjacent (or contiguous) to the function
are called adjacent (or contiguous) to the function  . There is a linear relationship between
. There is a linear relationship between 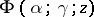 and any two functions adjacent to it, e.g.
and any two functions adjacent to it, e.g.
Six formulas of this type may be obtained from the relations between adjacent functions for hypergeometric functions. The successive use of these recurrence formulas yields linear relations connecting the function  with the associated functions
with the associated functions  , where
, where 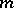 and
and  are integers.
are integers.
Differentiation formulas:
Basic integral representations.
The asymptotic behaviour of confluent hypergeometric functions as  can be studied using the integral representations [1], [2], [3]. If
can be studied using the integral representations [1], [2], [3]. If 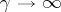 , while
, while 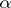 and
and  are bounded, the behaviour of the function
are bounded, the behaviour of the function  is described by formula (2). In particular, for large
is described by formula (2). In particular, for large 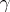 and bounded
and bounded 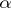 and
and  :
:
Representations of functions by confluent hypergeometric functions.
Bessel functions:
Laguerre polynomials:
Probability integrals:
The exponential integral function:
The logarithmic integral function:
Gamma-functions:
Elementary functions:
See also [1], [2], [3], [8].
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | I.S. Gradshtein, I.M. Ryzhik, "Table of integrals, series and products" , Acad. Press (1980) (Translated from Russian) |
| [3] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1964) |
| [4] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 |
| [5] | A.L. Lebedev, R.M. Fedorova, "Handbook of mathematical tables" , Moscow (1956) (In Russian) |
| [6] | N.M. Burunova, "Handbook of mathematical tables" , Moscow (1959) (In Russian) |
| [7] | A.A. Fletcher, J.C.P. Miller, L. Rosenhead, L.J. Comrie, "An index of mathematical tables" , 1–2 , Oxford Univ. Press (1962) |
| [8] | N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian) |
How to Cite This Entry:
Confluent hypergeometric function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Confluent_hypergeometric_function&oldid=17182
This article was adapted from an original article by E.A. Chistova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article


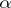 and
and 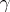 are parameters which assume any real or complex values except for
are parameters which assume any real or complex values except for  and
and  is a complex variable. The function
is a complex variable. The function 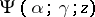 is called the confluent hypergeometric function of the first kind. The second linearly independent solution of equation (1),
is called the confluent hypergeometric function of the first kind. The second linearly independent solution of equation (1),
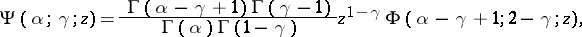
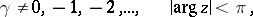
 is an entire analytic function in the entire complex
is an entire analytic function in the entire complex  -plane; if
-plane; if  is fixed, it is an entire function of
is fixed, it is an entire function of 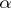 and a meromorphic function of
and a meromorphic function of 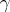 with simple poles at the points
with simple poles at the points  . The confluent hypergeometric function
. The confluent hypergeometric function 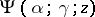 is an analytic function in the complex
is an analytic function in the complex  -plane with the slit
-plane with the slit 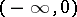 and an entire function of
and an entire function of  and
and  .
.
 is connected with the hypergeometric function
is connected with the hypergeometric function  by the relation
by the relation
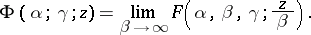
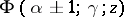 ,
,  are called adjacent (or contiguous) to the function
are called adjacent (or contiguous) to the function  . There is a linear relationship between
. There is a linear relationship between 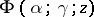 and any two functions adjacent to it, e.g.
and any two functions adjacent to it, e.g.
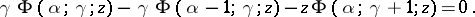
 with the associated functions
with the associated functions  , where
, where 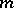 and
and  are integers.
are integers.

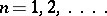


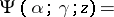

 can be studied using the integral representations [1], [2], [3]. If
can be studied using the integral representations [1], [2], [3]. If 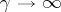 , while
, while 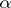 and
and  are bounded, the behaviour of the function
are bounded, the behaviour of the function  is described by formula (2). In particular, for large
is described by formula (2). In particular, for large 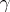 and bounded
and bounded 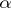 and
and  :
: