Implicit function
A function 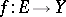 given by an equation
given by an equation 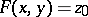 , where
, where 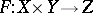 ,
, 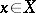 ,
, 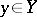 ,
, 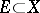 , and
, and 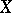 ,
, 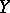 and
and 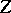 are certain sets, i.e. a function
are certain sets, i.e. a function 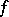 such that
such that 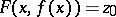 for any
for any 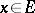 . If
. If 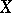 ,
, 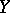 and
and 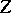 are topological spaces and if
are topological spaces and if 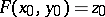 for some point
for some point  , then under certain conditions the equation
, then under certain conditions the equation 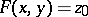 is uniquely solvable in one of the variables in some neighbourhood of
is uniquely solvable in one of the variables in some neighbourhood of 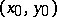 . Properties of the solution of this equation are described by implicit-function theorems.
. Properties of the solution of this equation are described by implicit-function theorems.
The simplest implicit-function theorem is as follows. Suppose that 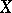 and
and 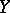 are subsets of the real line
are subsets of the real line 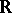 , let
, let 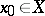 ,
, 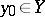 , and let
, and let 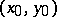 be an interior point of the plane set
be an interior point of the plane set  ; if
; if 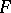 is continuous in some neighbourhood of
is continuous in some neighbourhood of 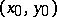 , if
, if 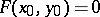 and if there are a
and if there are a 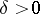 and an
and an 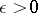 such that
such that 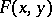 , for any fixed
, for any fixed 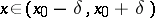 , is strictly monotone on
, is strictly monotone on 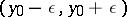 as a function of
as a function of 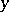 , then there is a
, then there is a 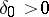 such that there is a unique function
such that there is a unique function
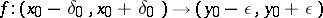 |
for which 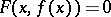 for all
for all 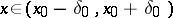 ; moreover,
; moreover, 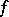 is continuous and
is continuous and  .
.
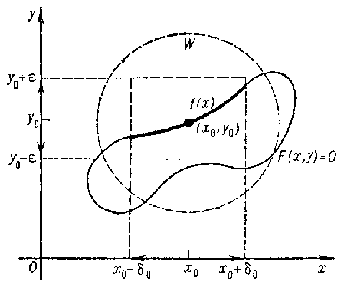
Figure: i050310a
The hypotheses of this theorem are satisfied if 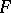 is continuous in a neighbourhood of
is continuous in a neighbourhood of 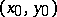 , if the partial derivative
, if the partial derivative 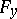 exists and is continuous at
exists and is continuous at 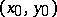 , if
, if 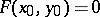 , and if
, and if 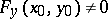 . If in addition the partial derivative
. If in addition the partial derivative 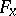 exists and is continuous at
exists and is continuous at 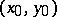 , then the implicit function
, then the implicit function 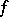 is differentiable at
is differentiable at 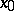 , and
, and
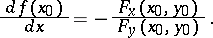 |
This theorem has been generalized to the case of a system of equations, that is, when 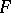 is a vector function. Let
is a vector function. Let 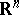 and
and  be
be  - and
- and  -dimensional Euclidean spaces with fixed coordinate systems and points
-dimensional Euclidean spaces with fixed coordinate systems and points 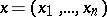 and
and 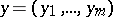 , respectively. Suppose that
, respectively. Suppose that 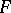 maps a certain neighbourhood
maps a certain neighbourhood 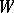 of
of 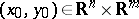 (
(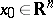 ,
, 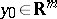 ) into
) into  and that
and that 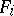 ,
,  , are the coordinate functions (of the
, are the coordinate functions (of the 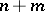 variables
variables 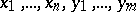 ) of
) of 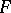 , that is,
, that is, 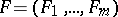 . If
. If 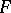 is differentiable on
is differentiable on  , if
, if 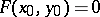 and if the Jacobian
and if the Jacobian
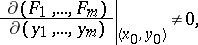 |
then there are neighbourhoods  and
and 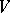 of
of  and
and 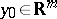 , respectively,
, respectively, 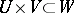 , and a unique mapping
, and a unique mapping 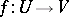 such that
such that  for all
for all  . Here
. Here  ,
, 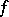 is differentiable on
is differentiable on 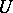 , and if
, and if 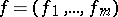 , then the explicit expression for the partial derivatives
, then the explicit expression for the partial derivatives 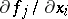 ,
, 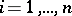 ,
, 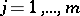 , can be found from the system of
, can be found from the system of  linear equations in these derivatives:
linear equations in these derivatives:
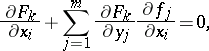 |
 ,
, 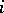 is fixed
is fixed 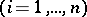 . Sometimes the main assertion of the theorem is stated as follows: There are neighbourhoods
. Sometimes the main assertion of the theorem is stated as follows: There are neighbourhoods  of
of  in
in 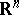 and
and 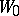 of
of 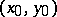 in
in 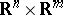 ,
, 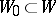 , and a unique mapping
, and a unique mapping 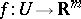 such that
such that 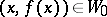 and
and 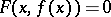 for all
for all 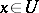 . In other words, the conditions
. In other words, the conditions
 |
are equivalent to 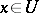 ,
, 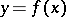 . In this case one says that the equation
. In this case one says that the equation 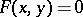 is uniquely solvable in the neighbourhood
is uniquely solvable in the neighbourhood 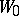 of
of  .
.
The classical implicit-function theorem thus stated generalizes to the case of more general spaces in the following manner. Let 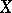 be a topological space, let
be a topological space, let 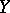 and
and 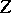 be affine normed spaces over the field of real or complex numbers, that is, affine spaces over the relevant field to which are associated normed vector spaces
be affine normed spaces over the field of real or complex numbers, that is, affine spaces over the relevant field to which are associated normed vector spaces 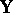 and
and 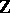 ,
,  being complete, let
being complete, let 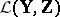 be the set of continuous linear mappings from
be the set of continuous linear mappings from  into
into 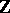 , and let
, and let 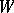 be an open set in the product space
be an open set in the product space  ,
, 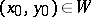 ,
, 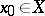 ,
, 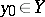 .
.
Let 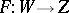 be a continuous mapping and
be a continuous mapping and  . If for every fixed
. If for every fixed  and
and  the mapping
the mapping  has a partial Fréchet derivative
has a partial Fréchet derivative 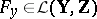 , if
, if 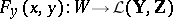 is a continuous mapping and if the linear mapping
is a continuous mapping and if the linear mapping 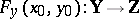 has a continuous inverse linear mapping (that is, it is an invertible element of
has a continuous inverse linear mapping (that is, it is an invertible element of 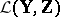 ), then there exist open sets
), then there exist open sets 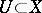 and
and 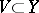 ,
, 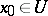 ,
, 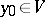 , such that for any
, such that for any 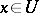 there is a unique element
there is a unique element  , denoted by
, denoted by  , satisfying the equations
, satisfying the equations
 |
The function 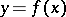 thus defined is a continuous mapping from
thus defined is a continuous mapping from 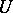 into
into 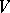 , and
, and 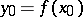 .
.
If 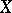 is also an affine normed space, then under certain conditions the implicit function
is also an affine normed space, then under certain conditions the implicit function 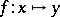 which satisfies the equation
which satisfies the equation
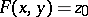 | (1) |
is also differentiable. Namely, let 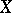 ,
, 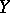 and
and 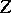 be affine normed spaces, let
be affine normed spaces, let 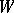 be an open set in
be an open set in 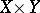 , let
, let 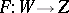 ,
, 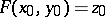 ,
, 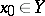 , and let
, and let  be the implicit mapping given by (1), taking a certain neighbourhood
be the implicit mapping given by (1), taking a certain neighbourhood 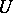 of
of 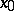 into an open subset
into an open subset 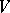 of
of  ,
, 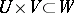 . Thus, for all
. Thus, for all 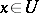 ,
,
 | (2) |
Suppose also that 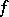 is continuous at
is continuous at 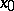 and that
and that 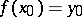 . If
. If 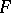 is differentiable at
is differentiable at 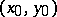 , if its partial Fréchet derivatives
, if its partial Fréchet derivatives 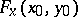 and
and 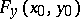 are continuous linear operators taking the vector spaces
are continuous linear operators taking the vector spaces 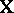 and
and  associated with
associated with 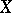 and
and 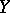 into the vector space
into the vector space 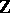 associated with
associated with 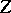 , and if the operator
, and if the operator 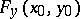 is an invertible element of
is an invertible element of 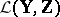 , then
, then 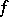 is differentiable at
is differentiable at 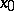 and its Fréchet derivative is given by
and its Fréchet derivative is given by
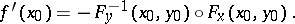 |
This is obtained as a result of formally differentiating (2):
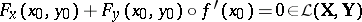 |
and multiplying this equality on the left by 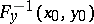 .
.
If in addition the mapping 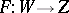 is continuously differentiable on
is continuously differentiable on 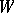 , if the implicit function
, if the implicit function 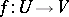 is continuous on
is continuous on 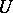 ,
, 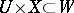 , and if for any
, and if for any 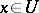 the partial Fréchet derivative
the partial Fréchet derivative 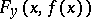 is an invertible element of
is an invertible element of  , then
, then 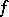 is a continuously-differentiable mapping of
is a continuously-differentiable mapping of 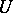 into
into 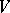 .
.
In the general case one can also indicate conditions for the existence and the uniqueness of the implicit function in terms of the continuity of the Fréchet derivative: If 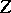 is complete, if the mapping
is complete, if the mapping 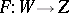 is continuously differentiable on
is continuously differentiable on 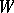 , if
, if 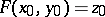 , and if the partial Fréchet derivative
, and if the partial Fréchet derivative 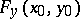 is an invertible element of
is an invertible element of 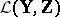 , then (1) is uniquely solvable in a sufficiently small neighbourhood of
, then (1) is uniquely solvable in a sufficiently small neighbourhood of  , i.e. there exist neighbourhoods
, i.e. there exist neighbourhoods 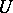 of
of 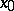 in
in 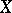 and
and 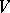 of
of 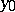 in
in 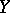 ,
,  , and a unique implicit function
, and a unique implicit function 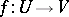 satisfying (2). Here
satisfying (2). Here  is also continuously differentiable on
is also continuously differentiable on  . In this form the implicit-function theorem for normed spaces is a direct generalization of the corresponding classic implicit-function theorem for a single scalar equation in two variables.
. In this form the implicit-function theorem for normed spaces is a direct generalization of the corresponding classic implicit-function theorem for a single scalar equation in two variables.
Furthermore, if 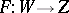 is a
is a 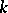 -times continuously-differentiable mapping in a neighbourhood
-times continuously-differentiable mapping in a neighbourhood  of
of 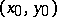 ,
, 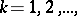 then the implicit function
then the implicit function 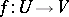 is also
is also 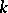 times continuously differentiable.
times continuously differentiable.
Far-reaching generalizations of the classic implicit-function theorem to differential operators were given by J. Nash (see Nash theorems (in differential geometry)).
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | L.A. Lyusternik, V.I. Sobolev, "Elemente der Funktionalanalysis" , Akademie Verlag (1968) (Translated from Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
| [4] | L. Schwartz, "Cours d'analyse" , 1 , Hermann (1967) |
| [5] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1 , MIR (1982) (Translated from Russian) |
Comments
References
| [a1] | W. Fleming, "Functions of several variables" , Addison-Wesley (1965) |
Implicit function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Implicit_function&oldid=17179