Binary relation
A two-place predicate on a given set. The term is sometimes used to denote a subset of the set  of ordered pairs
of ordered pairs  of elements of a given set
of elements of a given set  . A binary relation is a special case of a relation. Let
. A binary relation is a special case of a relation. Let  . If
. If  , then one says that the element
, then one says that the element  is in binary relation
is in binary relation  to the element
to the element  . An alternative notation for
. An alternative notation for  is
is  .
.
The empty subset 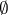 in
in  and the set
and the set  itself are called, respectively, the nil relation and the universal relation in the set
itself are called, respectively, the nil relation and the universal relation in the set  . The diagonal of the set
. The diagonal of the set  , i.e. the set
, i.e. the set  , is the equality relation or the identity binary relation in
, is the equality relation or the identity binary relation in  .
.
Let  be binary relations in a set
be binary relations in a set  . In addition to the set-theoretic operations of union
. In addition to the set-theoretic operations of union  , intersection
, intersection 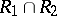 , and complementation
, and complementation 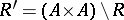 , one has the inversion
, one has the inversion
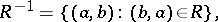 |
as well as the operation of multiplication:
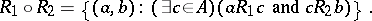 |
The binary relation 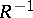 is said to be the inverse of
is said to be the inverse of  . Multiplication of binary relations is associative, but as a rule not commutative.
. Multiplication of binary relations is associative, but as a rule not commutative.
A binary relation 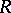 in
in 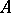 is said to be 1) reflexive if
is said to be 1) reflexive if  ; 2) transitive if
; 2) transitive if 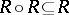 ; 3) symmetric if
; 3) symmetric if  ; and 4) anti-symmetric if
; and 4) anti-symmetric if  . If a binary relation has some of the properties 1), 2), 3) or 4), the inverse relation
. If a binary relation has some of the properties 1), 2), 3) or 4), the inverse relation 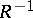 has these properties as well. The binary relation
has these properties as well. The binary relation  is said to be functional if
is said to be functional if 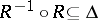 .
.
The most important types of binary relations are equivalences, order relations (total and partial), and functional relations (cf. Equivalence; Order relation; Functional relation).
Binary relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binary_relation&oldid=17163