Affine tensor
From Encyclopedia of Mathematics
An element of the tensor product of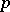 
copies of an 
-dimensional vector space 
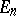and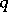 
copies of the dual vector space 
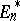. Such a tensor is said to be of type 
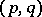, the number 
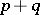defining the valency, or degree, of the tensor. Having chosen a basis 
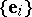in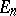 
, one defines an affine tensor of type 
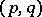with the aid of 
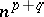components 
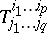which transform as a result of a change of basis 
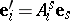according to the formula
 |
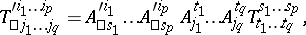where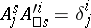 
. It is usually said that the tensor components undergo a contravariant transformation with respect to the upper indices, and a covariant transformation with respect to the lower.
Comments
An affine tensor as described above is commonly called simply a tensor.
References
| [a1] | B.A. Dubrovin, A.T. Fomenko, S.P. Novikov, "Modern geometry - methods and applications" , Springer (1984) (Translated from Russian) |
| [a2] | W.H. Greub, "Multilinear algebra" , Springer (1967) |
| [a3] | C.T.J. Dodson, T. Poston, "Tensor geometry" , Pitman (1977) |
How to Cite This Entry:
Affine tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_tensor&oldid=17159
Affine tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_tensor&oldid=17159
This article was adapted from an original article by A.P. Shirokov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article