Keldysh theorem
Keldysh' theorem on approximating continuous functions by polynomials. Let 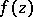 be a function of a complex variable
be a function of a complex variable  that is holomorphic in a domain
that is holomorphic in a domain 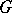 and continuous in the closed domain
and continuous in the closed domain 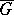 . Then in order that for any
. Then in order that for any 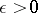 a polynomial
a polynomial 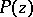 exists such that
exists such that
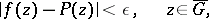 |
it is necessary and sufficient that the complement 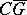 consists of a single domain
consists of a single domain 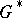 containing the point at infinity. The theorem was established by M.V. Keldysh . It is one of the basic results in the theory of uniform approximation of functions by polynomials in the complex domain (see ).
containing the point at infinity. The theorem was established by M.V. Keldysh . It is one of the basic results in the theory of uniform approximation of functions by polynomials in the complex domain (see ).
Keldysh' theorems in potential theory are theorems on the solvability of the Dirichlet problem, established by M.V. Keldysh in 1938–1941.
a) Let 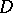 be a bounded domain in the Euclidean space
be a bounded domain in the Euclidean space 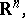
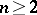 , with boundary
, with boundary 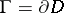 . Then there exists on
. Then there exists on 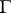 a countable set of irregular boundary points (cf. Irregular boundary point)
a countable set of irregular boundary points (cf. Irregular boundary point) 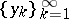 , such that the Dirichlet problem is solvable in
, such that the Dirichlet problem is solvable in 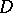 with a continuous boundary function
with a continuous boundary function 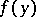 on
on 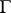 if and only if this problem is solvable at
if and only if this problem is solvable at 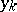 ,
, 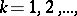 that is, if and only if
that is, if and only if
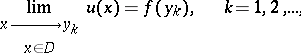 |
where 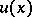 is the generalized solution of the Dirichlet problem in the sense of Wiener–Perron (see Perron method, and also [3], [4]).
is the generalized solution of the Dirichlet problem in the sense of Wiener–Perron (see Perron method, and also [3], [4]).
b) Let 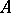 be an operator acting from the space
be an operator acting from the space 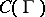 of continuous functions on
of continuous functions on 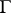 into the space of bounded harmonic functions (cf. Harmonic function) in
into the space of bounded harmonic functions (cf. Harmonic function) in 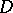 and satisfying the following conditions:
and satisfying the following conditions: 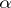 )
) 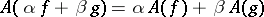 ,
, 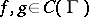 , where
, where  are real numbers; that is,
are real numbers; that is, 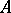 is linear;
is linear; 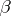 ) if
) if 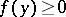 ,
, 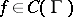 , then
, then 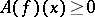 ; and
; and  ) if the Dirichlet problem is solvable for an
) if the Dirichlet problem is solvable for an 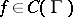 , then
, then 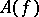 gives the solution of this problem. Under these conditions
gives the solution of this problem. Under these conditions 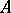 is unique for
is unique for 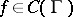 , and
, and 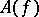 gives a generalized solution of the Dirichlet problem in the sense of Wiener–Perron (see [5]–[7]).
gives a generalized solution of the Dirichlet problem in the sense of Wiener–Perron (see [5]–[7]).
c) In order that each solvable Dirichlet problem in 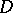 be stable in
be stable in 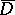 , it is necessary and sufficient that the set of irregular boundary points of
, it is necessary and sufficient that the set of irregular boundary points of 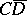 coincide with the set of irregular boundary points of
coincide with the set of irregular boundary points of  . The Dirichlet problem is stable in the interior of
. The Dirichlet problem is stable in the interior of 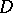 with respect to any function
with respect to any function 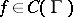 if and only if the set of irregular boundary points of
if and only if the set of irregular boundary points of 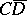 belonging to
belonging to 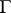 has zero harmonic measure in
has zero harmonic measure in 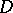 (see [4] or [6]).
(see [4] or [6]).
References
| [1] | M.V. Keldysh, "Sur la réprésentation par des séries de polynômes des fonctions d'une variable complexe dans des domaines fermés" Mat. Sb. , 16 : 3 (1945) pp. 249–258 |
| [2] | S.N. Mergelyan, "Uniform approximations to functions of a complex variable" Transl. Amer. Math. Soc. (1) , 3 (1962) pp. 294–391 Uspekhi Mat. Nauk , 7 : 2 (1952) pp. 3–122 |
| [3] | M.V. Keldysh, "Sur la résolubilité et la stabilité du problème de Dirichlet" Dokl. Akad. Nauk SSSR , 18 (1938) pp. 315–318 |
| [4] | M.V. Keldysh, "On the solvability and stability of the Dirichlet problem" Uspekhi Mat. Nauk , 8 (1941) pp. 171–231 (In Russian) |
| [5] | M.V. Keldysh, "Sur le problème de Dirichlet" Dokl. Akad. Nauk SSSR , 32 (1941) pp. 308–309 |
| [6] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [7] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
Comments
For Keldysh' approximation theorem see also [a2], Chapt. 30.
The operator 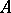 in b) is called a Keldysh operator. See [a1] for a treatment of Keldysh operators in axiomatic potential theory.
in b) is called a Keldysh operator. See [a1] for a treatment of Keldysh operators in axiomatic potential theory.
References
| [a1] | I. Netuka, "The classical Dirichlet problem and its generalizations" , Potential theory (Copenhagen, 1979) , Lect. notes in math. , 787 , Springer (1980) pp. 235–266 |
| [a2] | D. Gaier, "Lectures on complex approximation" , Birkhäuser (1987) (Translated from German) |
Keldysh theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Keldysh_theorem&oldid=17158