Affine connection
A differential-geometric structure on a smooth manifold 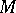 , a special kind of connection on a manifold (cf. Connections on a manifold), when the smooth fibre bundle
, a special kind of connection on a manifold (cf. Connections on a manifold), when the smooth fibre bundle 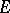 attached to
attached to 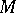 has the affine space
has the affine space 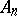 of dimension
of dimension  as its typical fibre. The structure of such an
as its typical fibre. The structure of such an 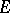 involves the assignment to each point
involves the assignment to each point  of a copy of the affine space
of a copy of the affine space 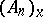 , which is identified with the tangent centro-affine space
, which is identified with the tangent centro-affine space 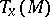 . In an affine connection each smooth curve
. In an affine connection each smooth curve 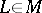 with origin
with origin 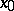 and each one of its points
and each one of its points 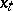 is thus provided with an affine mapping
is thus provided with an affine mapping 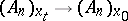 which satisfies the condition formulated below. Let
which satisfies the condition formulated below. Let 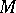 be covered with coordinate domains, each provided with a smooth field of affine frames in
be covered with coordinate domains, each provided with a smooth field of affine frames in 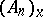 . The origin of these frames coincides with
. The origin of these frames coincides with  (i.e.
(i.e.  smooth vector fields, linearly independent at each point
smooth vector fields, linearly independent at each point  of the domain, are given). The requirement is that, as
of the domain, are given). The requirement is that, as 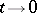 , when
, when 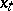 moves along
moves along 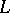 towards
towards  , the mapping
, the mapping 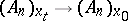 tends to become the identity mapping, and that the principal part of its deviation from the identity mapping be defined, with respect to some frame, by the system of linear differential forms
tends to become the identity mapping, and that the principal part of its deviation from the identity mapping be defined, with respect to some frame, by the system of linear differential forms
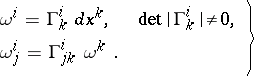 | (1) |
Thus, for 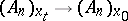 , the image of the frame at
, the image of the frame at 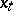 is the system consisting of the point in
is the system consisting of the point in 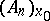 with position vector
with position vector  and
and  vectors
vectors 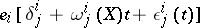 , where
, where 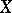 is the tangent vector to
is the tangent vector to  at
at 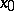 , and
, and
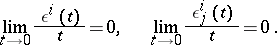 |
A manifold 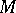 with an affine connection defined on it is called a space with an affine connection. During the transformation of a frame of the field at an arbitrary point
with an affine connection defined on it is called a space with an affine connection. During the transformation of a frame of the field at an arbitrary point 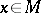 according to the formulas
according to the formulas 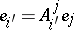 ,
, 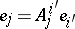 , i.e. when passing to an arbitrary element of the principal fibre bundle
, i.e. when passing to an arbitrary element of the principal fibre bundle 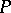 of frames in the tangent spaces
of frames in the tangent spaces 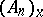 with origins at the point
with origins at the point  , the forms (1) are replaced by the following
, the forms (1) are replaced by the following 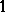 -forms on
-forms on 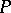 :
:
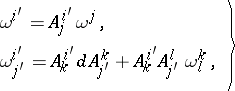 | (2) |
while the  -forms
-forms
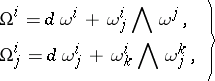 | (3) |
are transformed as follows:
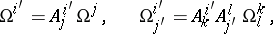 |
where 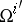 and
and 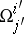 are composed from the forms (2) according to (3). The equations (3) are called the structure equations of the affine connection on
are composed from the forms (2) according to (3). The equations (3) are called the structure equations of the affine connection on 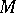 . Here the left-hand sides — the so-called torsion forms
. Here the left-hand sides — the so-called torsion forms 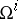 and curvature forms
and curvature forms 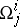 — are semi-basic (cf. Torsion form; Curvature form), i.e. they are linear combinations of the
— are semi-basic (cf. Torsion form; Curvature form), i.e. they are linear combinations of the 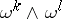 :
:
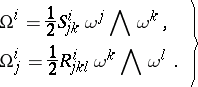 | (4) |
All 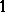 -forms
-forms 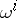 and
and 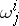 , defined on
, defined on 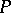 and satisfying equations (3) with left-hand sides of type (4), define a certain affine connection on
and satisfying equations (3) with left-hand sides of type (4), define a certain affine connection on 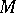 . The mapping
. The mapping 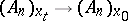 for a curve
for a curve 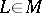 is obtained as follows. A smooth field of frames is chosen in a coordinate neighbourhood of the origin
is obtained as follows. A smooth field of frames is chosen in a coordinate neighbourhood of the origin 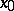 of the curve
of the curve 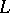 , and the image of the frame at point
, and the image of the frame at point 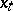 is defined as the solution
is defined as the solution 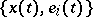 of the system
of the system
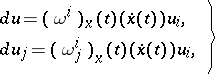 | (5) |
for the initial conditions 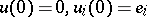 , where
, where 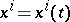 are the defining equations of the curve
are the defining equations of the curve 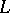 . The curve which is described in
. The curve which is described in 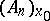 by the point with position vector
by the point with position vector  with respect to
with respect to 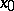 is known as the development of
is known as the development of 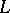 . The field of frames in the coordinate neighbourhood may be so chosen that
. The field of frames in the coordinate neighbourhood may be so chosen that 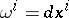 ; then
; then 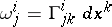 . In the intersection of the coordinate neighbourhoods,
. In the intersection of the coordinate neighbourhoods, 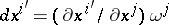 , i.e.
, i.e. 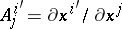 and
and
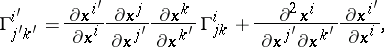 | (6) |
 | (7) |
Here 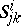 and
and  are, respectively, the torsion tensor and the curvature tensor of the affine connection on
are, respectively, the torsion tensor and the curvature tensor of the affine connection on 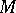 . An affine connection on
. An affine connection on 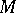 may be defined by a system of functions
may be defined by a system of functions 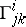 on each coordinate neighbourhood which transforms in the intersection of two neighbourhoods according to formula (5). The system
on each coordinate neighbourhood which transforms in the intersection of two neighbourhoods according to formula (5). The system 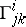 is called the object of the affine connection. The mapping
is called the object of the affine connection. The mapping 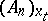 is obtained with the aid of (5) into which
is obtained with the aid of (5) into which
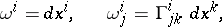 |
is to be substituted.
If, in some neighbourhood of the point 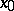 , a vector field
, a vector field 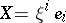 is given, then, when
is given, then, when 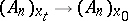 , the vector
, the vector 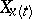 is mapped into the vector
is mapped into the vector 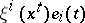 (where
(where 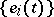 is the solution of system (5)). The differential of this in
is the solution of system (5)). The differential of this in 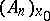 at
at 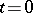 :
:
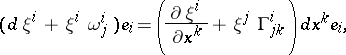 |
is called the covariant differential of the field 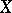 with respect to the given affine connection. Here
with respect to the given affine connection. Here
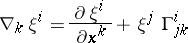 |
form a tensor field, called the covariant derivative of the field 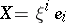 . If a second vector field
. If a second vector field 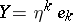 is given, the covariant derivative of the field
is given, the covariant derivative of the field 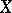 in the direction of
in the direction of 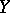 is defined as
is defined as
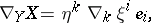 |
which may also be defined with respect to an arbitrary field of frames by the formula
 |
An affine connection on 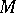 may also be defined as a bilinear operator
may also be defined as a bilinear operator  which assigns a vector field
which assigns a vector field 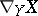 to each two vector fields
to each two vector fields 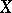 and
and 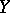 , and which possesses the properties:
, and which possesses the properties:
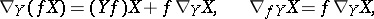 |
where 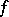 is a smooth function on
is a smooth function on 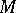 . The relation between these definitions is established by the formula
. The relation between these definitions is established by the formula 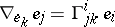 where
where 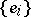 is the field of frames. The fields of the torsion tensor and curvature tensor
is the field of frames. The fields of the torsion tensor and curvature tensor
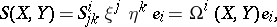 |
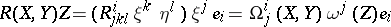 |
are defined by the formulas:
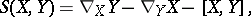 |
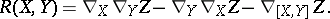 |
A vector field 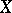 is said to be parallel along the curve
is said to be parallel along the curve 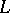 if
if 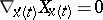 holds identically with respect to
holds identically with respect to 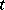 , i.e. if, along
, i.e. if, along 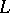 ,
,
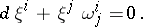 |
Parallel vector fields are used to effect parallel displacement of vectors (and, generally, of tensors) in an affine connection, representing a linear mapping of the tangent vector spaces 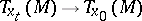 , defined by the mapping
, defined by the mapping 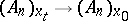 . In this sense any affine connection generates a linear connection on
. In this sense any affine connection generates a linear connection on 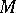 .
.
A curve 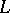 is called a geodesic line in a given affine connection if its development is a straight line; in other words, if, by a suitable parametrization, its tangent vector field
is called a geodesic line in a given affine connection if its development is a straight line; in other words, if, by a suitable parametrization, its tangent vector field 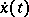 is parallel to it. Geodesic lines are defined with respect to a local coordinate system by the system
is parallel to it. Geodesic lines are defined with respect to a local coordinate system by the system
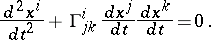 |
Through each point, in each direction passes one geodesic line.
There is a one-to-one correspondence between affine connections on  and connections in principal fibre bundles of free affine frames in
and connections in principal fibre bundles of free affine frames in 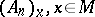 , generated by them. To closed curves with origin and end at
, generated by them. To closed curves with origin and end at  there correspond affine transformations
there correspond affine transformations 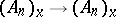 , which form the non-homogeneous holonomy group of the given affine connection. The corresponding linear automorphisms
, which form the non-homogeneous holonomy group of the given affine connection. The corresponding linear automorphisms 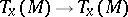 form the homogeneous holonomy group. In accordance with the holonomy theorem, the Lie algebras of these groups are defined by the
form the homogeneous holonomy group. In accordance with the holonomy theorem, the Lie algebras of these groups are defined by the  -forms of torsion
-forms of torsion 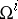 and curvature
and curvature 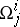 . The Bianchi identities apply to the latter:
. The Bianchi identities apply to the latter:
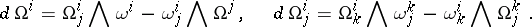 |
In particular, for torsion-free affine connections, when 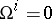 , these identities reduce to the following:
, these identities reduce to the following:
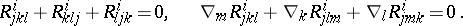 |
The concept of an affine connection arose in 1917 in Riemannian geometry (in the form of the Levi-Civita connection); it found an independent meaning in 1918–1924 owing to work of H. Weyl [1] and E. Cartan .
References
| [1] | H. Weyl, "Raum, Zeit, Materie" , Springer (1923) |
| [2a] | E. Cartan, "Sur les variétés a connexion affine et la théorie de la relativité généralisée (première partie)" Ann. Sci. École Norm. Sup. , 40 (1923) pp. 325–412 |
| [2b] | E. Cartan, "Sur les variétés a connexion affine et la théorie de la relativité généralisée (première partie suite)" Ann. Sci. École Norm. Sup. , 41 (1924) pp. 1–25 |
| [2c] | E. Cartan, "Sur les variétés a connexion affine et la théorie de la relativité généralisée (deuxième partie)" Ann. Sci. École Norm. Sup. , 42 (1925) pp. 17–88 |
| [3a] | E. Cartan, "Sur les variétés à connexion projective" Bull. Soc. Math. France , 52 (1924) pp. 205–241 |
| [3b] | E. Cartan, "Sur les espaces à connexion conforme" Ann. Soc. Polon. Math. , 2 (1923) pp. 171–221 |
| [4] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [5] | M.M. Postnikov, "The variational theory of geodesics" , Saunders (1967) (Translated from Russian) |
Comments
Instead of the articles [3a], [3b], one may consult [a1]. Useful additional up-to-date references in English are [a2] and [a3].
References
| [a1] | A. Lichnerowicz, "Théorie globale des connexions et des groupes d'holonomie" , Cremonese (1955) |
| [a2] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963) |
| [a3] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
Affine connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_connection&oldid=17102