Student test

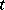-test

A significance test for the mean value of a normal distribution.

The single-sample Student test.

Let the independent random variables 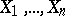be subject to the normal law 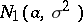, the parameters and 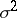of which are unknown, and let a simple hypothesis : 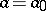be tested against the composite alternative 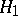: 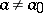. In solving this problem, a Student test is used, based on the statistic

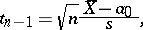where

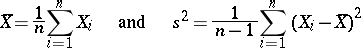are estimators of the parameters and 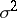, calculated with respect to the sample 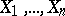. When 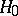is correct, the statistic 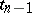is subject to the Student distribution with 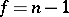degrees of freedom, i.e.

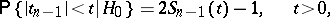where 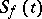is the Student distribution function with degrees of freedom. According to the single-sample Student test with significance level , , 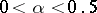the hypothesis 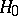must be accepted if

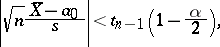where 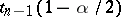is the quantile of level 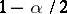of the Student distribution with 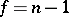degrees of freedom, i.e. 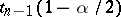is the solution of the equation 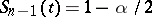. On the other hand, if

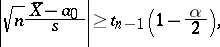then, according to the Student test of level 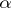, the tested hypothesis 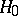: 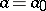has to be rejected, and the alternative hypothesis 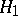: 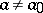has to be accepted.

The two-sample Student test.

Let and 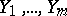be mutually independent normally-distributed random variables with the same unknown variance 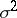, and let

where the parameters 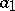and 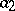are also unknown (it is often said that there are two independent normal samples). Moreover, let the hypothesis 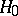: be tested against the alternative 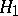: 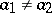. In this instance, both hypotheses are composite. Using the observations 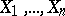and 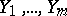it is possible to calculate the estimators

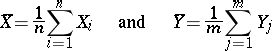for the unknown mathematical expectations 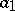and 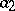, as well as the estimators

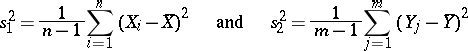for the unknown variance 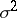. Moreover, let

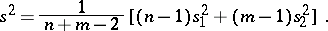Then, when 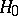is correct, the statistic

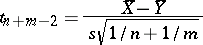is subject to the Student distribution with 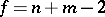degrees of freedom. This fact forms the basis of the two-sample Student test for testing 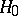against 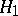. According to the two-sample Student test of level 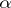, , 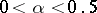the hypothesis 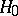is accepted if

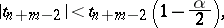where 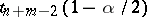is the quantile of level 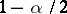of the Student distribution with 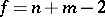degrees of freedom. If

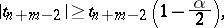then, according to the Student test of level 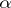, the hypothesis 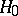is rejected in favour of .

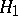References

[1]	H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946)
[2]	S.S. Wilks, "Mathematical statistics" , Wiley (1962)
[3]	N.V. Smirnov, I.V. Dunin-Barkovskii, "Mathematische Statistik in der Technik" , Deutsch. Verlag Wissenschaft. (1969) (Translated from Russian)
[4]	L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)
[5]	Yu.V. Linnik, "Methoden der kleinsten Quadraten in moderner Darstellung" , Deutsch. Verlag Wissenschaft. (1961) (Translated from Russian)