Standard simplex
The simplex  of dimension
of dimension  in the space
in the space  with vertices at the points
with vertices at the points  ,
,  (the
(the 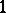 stands in the
stands in the  -th place), i.e.
-th place), i.e.
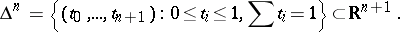 |
For any topological space  , the continuous mappings
, the continuous mappings 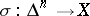 are the singular simplices of
are the singular simplices of 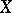 (see Singular homology).
(see Singular homology).
The simplicial complex 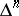 whose vertices are the points
whose vertices are the points 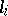 ,
, 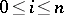 , while the simplices are arbitrary non-empty subsets of vertices. The geometric realization of this simplicial complex coincides with the standard simplex in the sense of 1).
, while the simplices are arbitrary non-empty subsets of vertices. The geometric realization of this simplicial complex coincides with the standard simplex in the sense of 1).
The simplicial set  , obtained by applying the functor
, obtained by applying the functor 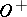 to the simplicial scheme in 2), which is a contra-variant functor on the category
to the simplicial scheme in 2), which is a contra-variant functor on the category 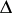 (see Simplicial object in a category), for which
(see Simplicial object in a category), for which
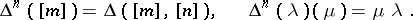 |
Thus, non-decreasing sequences  of numbers from
of numbers from 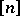 are
are  -dimensional simplices of the simplicial set
-dimensional simplices of the simplicial set 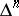 , while the face operators
, while the face operators 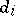 and the degeneracy operators
and the degeneracy operators 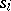 of this simplicial set are defined by the formulas
of this simplicial set are defined by the formulas
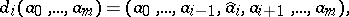 |
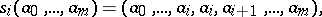 |
where the sign  signifies that the symbol beneath it is deleted. The simplicial set
signifies that the symbol beneath it is deleted. The simplicial set  is also called a simplicial segment. The simplex
is also called a simplicial segment. The simplex  (the unique non-degenerate
(the unique non-degenerate  -dimensional simplex of
-dimensional simplex of 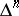 ) is called the fundamental simplex of
) is called the fundamental simplex of 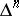 . The smallest simplicial subset of
. The smallest simplicial subset of 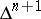 containing all simplices of the form
containing all simplices of the form 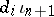 with
with 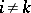 is denoted by
is denoted by 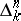 and is called the
and is called the 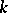 -th standard horn.
-th standard horn.
For any simplicial set 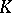 and an arbitrary
and an arbitrary  -dimensional simplex
-dimensional simplex  of
of 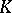 , there is a unique simplicial mapping
, there is a unique simplicial mapping 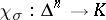 for which
for which 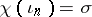 . This mapping is said to be characteristic for
. This mapping is said to be characteristic for 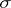 .
.
The fundamental simplex 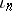 of a simplicial set as in 3), which in this instance is denoted by
of a simplicial set as in 3), which in this instance is denoted by  .
.
Comments
For references see Simplicial set.
Standard simplex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Standard_simplex&oldid=17060