Orthogonalization

orthogonalization process

An algorithm to construct for a given linear independent system of vectors in a Euclidean or Hermitian space an orthogonal system of non-zero vectors generating the same subspace in . The most well-known is the Schmidt (or Gram–Schmidt) orthogonalization process, in which from a linear independent system , an orthogonal system is constructed such that every vector () is linearly expressed in terms of , i.e. , where is an upper-triangular matrix. It is possible to construct the system such that it is orthonormal and such that the diagonal entries 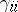of 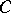are positive; the system 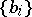and the matrix 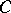are defined uniquely by these conditions.

The Gram–Schmidt process is as follows. Put 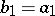; if the vectors 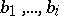have already been constructed, then

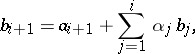where

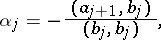, are obtained from the condition of orthogonality of the vector to 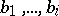. The geometric sense of this process comprises the fact that at every step, the vector 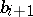is perpendicular to the linear hull of drawn to the end of the vector 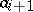. The product of the lengths 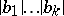is equal to the volume of the parallelepiped constructed on the vectors of the system as edges. By normalizing the vectors , the required orthonormal system is obtained. An explicit expression of the vectors in terms of is given by the formula

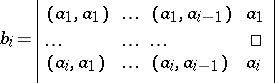(the determinant at the right-hand side has to be formally expanded by the last column). The corresponding orthonormal system takes the form

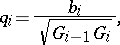where is the Gram determinant of the system .

This process can also be used for a countable system of vectors.

The Gram–Schmidt process can be interpreted as expansion of a non-singular square matrix in the product of an orthogonal (or unitary, in the case of a Hermitian space) and an upper-triangular matrix with positive diagonal entries, this product being a particular example of an Iwasawa decomposition.

References

[1]	F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian)
[2]	A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian)