Chebyshev–Laguerre polynomials
Polynomials that are orthogonal on the interval  with weight function
with weight function  , where
, where  . The standardized Laguerre polynomials are defined by the formula
. The standardized Laguerre polynomials are defined by the formula
Their representation by means of the gamma-function is
In applications the most important formulas are:
The polynomial  satisfies the differential equation (Laguerre equation)
satisfies the differential equation (Laguerre equation)
The generating function of the Laguerre polynomials has the form
The orthonormal Laguerre polynomials can be expressed in terms of the standardized polynomials as follows:
The set of all Laguerre polynomials is dense in the space of functions whose square is integrable with weight  on the interval
on the interval  .
.
Laguerre polynomials are most frequently used under the condition 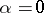 ; these were investigated by E. Laguerre [1], and are denoted in this case by
; these were investigated by E. Laguerre [1], and are denoted in this case by  (in contrast to them, the
(in contrast to them, the  are sometimes known as generalized Laguerre polynomials). The first few Laguerre polynomials
are sometimes known as generalized Laguerre polynomials). The first few Laguerre polynomials  have the form
have the form
The Laguerre polynomial 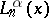 is sometimes denoted by
is sometimes denoted by  .
.
References
| [1] | E. Laguerre, "Sur le transformations des fonctions elliptiques" Bull. Soc. Math. France , 6 (1878) pp. 72–78 |
| [2] | V.A. Steklov, Izv. Imp. Akad. Nauk. , 10 (1916) pp. 633–642 |
| [3] | G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975) |
| [4] | P.K. Suetin, "Classical orthogonal polynomials" , Moscow (1979) (In Russian) |
Laguerre polynomials can be written as confluent hypergeometric functions (cf. Confluent hypergeometric function) and belong to the classical orthogonal polynomials. They have a close connection with the Heisenberg representation: as matrix elements of irreducible representations and as spherical functions on certain Gel'fand pairs (cf. Gel'fand representation) associated with the Heisenberg group. See the references given in [a1], Chapt. 1, §9.
References
| [a1] | G.B. Folland, "Harmonic analysis in phase space" , Princeton Univ. Press (1989) |
How to Cite This Entry:
Laguerre polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laguerre_polynomials&oldid=17042
This article was adapted from an original article by P.K. Suetin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article with weight function
with weight function  , where
, where  . The standardized Laguerre polynomials are defined by the formula
. The standardized Laguerre polynomials are defined by the formula
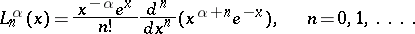
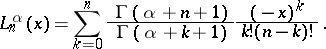
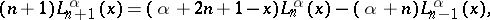
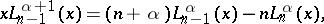
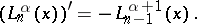
 satisfies the differential equation (Laguerre equation)
satisfies the differential equation (Laguerre equation)
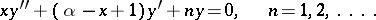
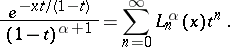
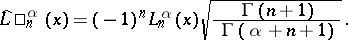
 on the interval
on the interval  .
.
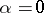 ; these were investigated by E. Laguerre [1], and are denoted in this case by
; these were investigated by E. Laguerre [1], and are denoted in this case by  (in contrast to them, the
(in contrast to them, the  are sometimes known as generalized Laguerre polynomials). The first few Laguerre polynomials
are sometimes known as generalized Laguerre polynomials). The first few Laguerre polynomials  have the form
have the form
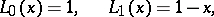
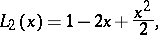
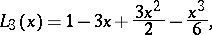
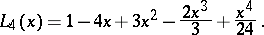
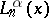 is sometimes denoted by
is sometimes denoted by  .
.