Fundamental group
Poincaré group
The first absolute homotopy group  . Let
. Let  be the interval
be the interval  , and let
, and let  be its boundary. The elements of the fundamental group of the pointed topological space
be its boundary. The elements of the fundamental group of the pointed topological space  are the homotopy classes of closed paths in
are the homotopy classes of closed paths in  , that is, homotopy classes
, that is, homotopy classes  of continuous mappings of the pair
of continuous mappings of the pair  into
into  . The path
. The path 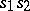 :
:
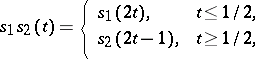 |
is called the product of 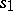 and
and 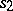 . The homotopy class of the product depends only on the classes of the factors, and the resulting operation is, generally speaking, non-commutative. The identity is the class of the constant mapping into
. The homotopy class of the product depends only on the classes of the factors, and the resulting operation is, generally speaking, non-commutative. The identity is the class of the constant mapping into 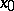 , and the inverse of the class
, and the inverse of the class 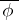 containing the path
containing the path  is the class of the path
is the class of the path  . To a continuous mapping
. To a continuous mapping 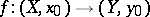 corresponds the homomorphism
corresponds the homomorphism
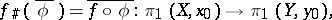 |
that is,  is a functor from the category of pointed topological spaces into the category of (non-Abelian) groups. For any path
is a functor from the category of pointed topological spaces into the category of (non-Abelian) groups. For any path 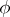 joining the points
joining the points  and
and  , one can define an isomorphism
, one can define an isomorphism
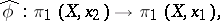 |
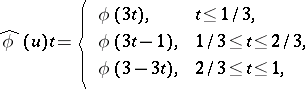 |
that depends only on the homotopy class of 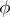 . The group
. The group  acts as a group of automorphisms on
acts as a group of automorphisms on 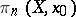 , and in the case
, and in the case  ,
,  acts as an inner automorphism
acts as an inner automorphism  . The Hurewicz homomorphism
. The Hurewicz homomorphism  is an epimorphism with kernel
is an epimorphism with kernel  (Poincaré's theorem).
(Poincaré's theorem).
A path-connected topological space with a trivial fundamental group is called simply connected. The fundamental group of a product of spaces  is isomorphic to the direct product of the fundamental groups of the factors:
is isomorphic to the direct product of the fundamental groups of the factors: 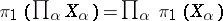 . Let
. Let  be a path-connected topological space, and let
be a path-connected topological space, and let 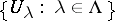 be a covering of
be a covering of 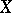 by a system of open sets
by a system of open sets 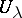 , closed under intersection, such that
, closed under intersection, such that 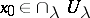 ; then
; then  is the direct limit of the diagram
is the direct limit of the diagram  , where
, where  , and
, and  is induced by the inclusion
is induced by the inclusion 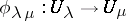 (the Seifert–van Kampen theorem). For example, if one is given a covering consisting of
(the Seifert–van Kampen theorem). For example, if one is given a covering consisting of  ,
,  and
and  , and if
, and if  is simply connected, then
is simply connected, then  is the free product of
is the free product of  and
and  . In the case of a CW-complex, the assertion of the theorem is also true for closed CW-subspaces of
. In the case of a CW-complex, the assertion of the theorem is also true for closed CW-subspaces of 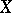 .
.
For a CW-complex  whose zero-dimensional skeleton consists of a single point
whose zero-dimensional skeleton consists of a single point  , each one-dimensional cell
, each one-dimensional cell 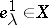 gives a generator of
gives a generator of 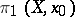 , and each two-dimensional cell
, and each two-dimensional cell 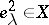 gives a relation corresponding to the attaching mapping of
gives a relation corresponding to the attaching mapping of  .
.
Suppose that  has a covering
has a covering  such that the inclusion homomorphism
such that the inclusion homomorphism 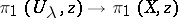 is zero for every point
is zero for every point  . Then there is a covering
. Then there is a covering  with
with 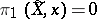 . In this case the group of homeomorphisms of
. In this case the group of homeomorphisms of  onto itself that commute with
onto itself that commute with  (covering transformations) is isomorphic to
(covering transformations) is isomorphic to 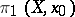 , and the order of
, and the order of 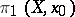 is equal to the cardinality of the fibre
is equal to the cardinality of the fibre 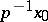 . For a mapping
. For a mapping  of path-connected spaces such that
of path-connected spaces such that 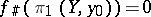 there is a lifting
there is a lifting 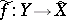 ,
, 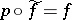 . The covering
. The covering 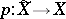 is called universal.
is called universal.
References
| [1] | W.S. Massey, "Algebraic topology: an introduction" , Springer (1977) |
| [2] | V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian) |
| [3] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [4] | J.R. Stallings, "Group theory and three-dimensional manifolds" , Yale Univ. Press (1972) |
Comments
References
| [a1] | B. Gran, "Homology theory" , Acad. Press (1975) |
Fundamental group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fundamental_group&oldid=17041