Pedal curve
of a curve 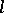 with respect to a point
with respect to a point 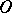
The set of bases to the perpendiculars dropped from the point 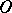 to the tangents to the curve
to the tangents to the curve 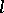 . For example, the Pascal limaçon is the pedal of a circle with respect to the point
. For example, the Pascal limaçon is the pedal of a circle with respect to the point 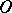 (see Fig.). The pedal (curve) of a plane curve
(see Fig.). The pedal (curve) of a plane curve  relative to the coordinate origin is
relative to the coordinate origin is
 |

Figure: p071950a
The equation for the pedal of a curve 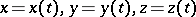 in space relative to the origin is
in space relative to the origin is
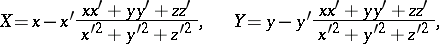 |
 |
The antipedal of a curve 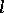 with respect to a point
with respect to a point 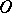 is the name given to the curve with as pedal, with respect to the point
is the name given to the curve with as pedal, with respect to the point 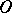 , the curve
, the curve 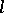 .
.
The pedal of a surface with respect to a point 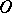 is the set of bases to the perpendiculars dropped from the point
is the set of bases to the perpendiculars dropped from the point 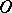 to the tangent planes to the surface. The equation for the pedal of a surface
to the tangent planes to the surface. The equation for the pedal of a surface 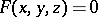 with respect to the coordinate origin is
with respect to the coordinate origin is
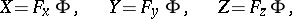 |
where
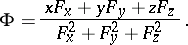 |
Comments
References
| [a1] | M. Berger, "Geometry" , I , Springer (1987) |
| [a2] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1–4 , Gauthier-Villars (1887–1896) |
Pedal curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pedal_curve&oldid=17030