De Rham cohomology

of an algebraic variety

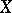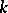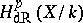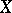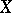A cohomology theory of algebraic varieties based on differential forms. To every algebraic variety over a field is associated a complex of regular differential forms (see Differential form on an algebraic variety); its cohomology groups are called the de Rham cohomology groups of . If is a smooth complete variety and if 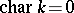, then de Rham cohomology is a special case of Weil cohomology (see [2], [3]). If 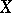is a smooth affine variety and if 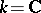, then the following analogue of the de Rham theorem is valid:

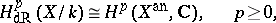where 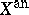is the complex-analytic manifold corresponding to the algebraic variety 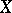(see [1]). For example, if 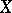is the complement of an algebraic hypersurface in 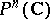, then the cohomology group 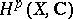can be calculated using rational differential forms on 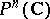with poles on this hypersurface.

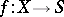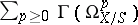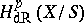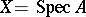For any morphism it is possible to define the relative de Rham complex (see Derivations, module of), which results in the relative de Rham cohomology groups . If and 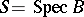are affine, the relative de Rham complex coincides with 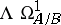. The cohomology groups 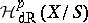of the sheaf complex 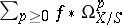on 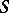are called the relative de Rham cohomology sheaves. These sheaves are coherent on 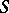if 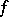is a proper morphism.

References

[1]	A. Grothendieck, "On the de Rham cohomology of algebraic varieties" Publ. Math. IHES , 29 (1966) pp. 351–359
[2]	R. Hartshorne, "Ample subvarieties of algebraic varieties" , Springer (1970)
[3]	R. Hartshorne, "On the de Rham cohomology of algebraic varieties" Publ. Math. IHES , 45 (1975) pp. 5–99