Unipotent group

A subgroup 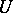of a linear algebraic group 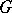consisting of unipotent elements (cf. Unipotent element). If 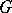is identified with its image under an isomorphic imbedding in a group 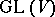of automorphisms of a suitable finite-dimensional vector space 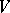, then a unipotent group is a subgroup contained in the set

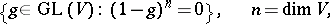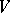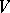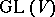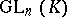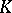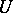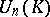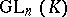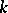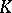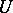of all unipotent automorphisms of . Fixing a basis in , one may identify with the general linear group , where is an algebraically closed ground field; the linear group is then also called a unipotent group. An example of a unipotent group is the group of all upper-triangular matrices in with 1's on the main diagonal. If is a subfield of and is a unipotent subgroup in 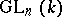, then 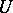is conjugate over 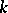to some subgroup of 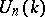. In particular, all elements of 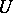have in 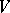a common non-zero fixed vector, and 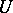is a nilpotent group. This theorem shows that the unipotent algebraic groups are precisely the Zariski-closed subgroups of 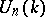for varying .

In any linear algebraic group 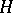there is a unique connected normal unipotent subgroup 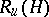(the unipotent radical) with reductive quotient group 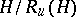(cf. Reductive group). To some extent this reduces the study of the structure of arbitrary groups to a study of the structure of reductive and unipotent groups. In contrast to the reductive case, the classification of unipotent algebraic groups is at present (1992) unknown.

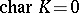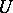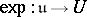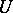Every subgroup and quotient group of a unipotent algebraic group is again unipotent. If , then is always connected; moreover, the exponential mapping (where is the Lie algebra of ) is an isomorphism of algebraic varieties; if 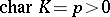, then there exist non-connected unipotent algebraic groups: e.g. the additive group 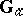of the ground field (which may be identified with 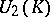) is a 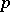-group and so contains a finite unipotent group. In a connected unipotent group 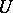there is a sequence of normal subgroups 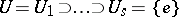such that all quotients 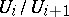are one-dimensional. Every connected one-dimensional unipotent algebraic group is isomorphic to 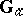. This reduces the study of connected unipotent algebraic groups to a description of iterated extensions of groups of type .

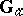Much more is known about commutative unipotent algebraic groups (cf. [4]) than in the general case. If 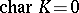, then they are precisely the algebraic groups isomorphic to 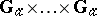; here, the isomorphism is given by the exponential mapping. If 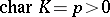, then the connected commutative unipotent algebraic groups 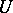are precisely the connected commutative algebraic 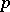-groups. Now 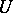need not be isomorphic to 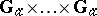: for this it is necessary and sufficient that 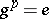for all 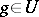. In the general case 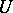is isogenous (cf. Isogeny) to a product of certain special groups (so-called Witt groups, cf. [2]).

If 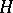and 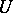are connected unipotent algebraic groups and 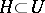, then the variety 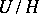is isomorphic to an affine space. Any orbit of a unipotent algebraic group of automorphisms of an affine algebraic variety 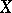is closed in 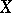[5].

References

[1]	A. Borel, "Linear algebraic groups" , Springer (1991)
[2]	J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959)
[3]	J.E. Humphreys, "Linear algebraic groups" , Springer (1981)
[4]	T. Kambayachi, M. Miyanishi, M. Takeuchi, "Unipotent algebraic groups" , Springer (1974)
[5]	R. Steinberg, "Conjugacy classes in algebraic groups" , Lect. notes in math. , 366 , Springer (1974)