Field
A commutative, associative ring containing a unit in which the set of non-zero elements is not empty and forms a group under multiplication (cf. Associative rings and algebras). A field may also be characterized as a simple non-zero commutative, associative ring containing a unit. Examples of fields: the field of rational numbers 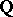 , the field of real numbers
, the field of real numbers 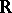 , the field of complex numbers
, the field of complex numbers 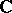 , finite fields (see Galois field), and the field of fractions of an integral domain.
, finite fields (see Galois field), and the field of fractions of an integral domain.
A subfield of a field 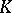 is a subset
is a subset 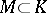 which itself is a field under the operations of addition and multiplication defined in
which itself is a field under the operations of addition and multiplication defined in 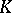 . For example, if
. For example, if 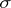 is some automorphism of a field
is some automorphism of a field 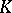 , then the set
, then the set
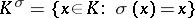 |
is a subfield in 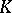 . If
. If 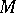 and
and 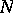 are subfields of a field
are subfields of a field 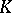 , then their intersection
, then their intersection 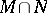 is a subfield in
is a subfield in 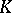 ; also, there exists a smallest subfield
; also, there exists a smallest subfield 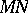 in the field
in the field 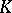 that contains
that contains 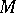 and
and 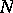 , called the composite of the fields
, called the composite of the fields 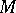 and
and 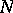 (in
(in 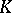 ). Each field contains a unique prime subfield (i.e. one not containing proper subfields).
). Each field contains a unique prime subfield (i.e. one not containing proper subfields).
Any field homomorphism is an imbedding. For an arbitrary field 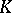 there exists a unique homomorphism
there exists a unique homomorphism 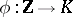 which maps the unit of the ring
which maps the unit of the ring 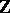 to the unit of the field
to the unit of the field 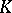 . If
. If 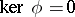 ,
, 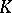 is called a field of characteristic zero. In that case, the prime subfield of
is called a field of characteristic zero. In that case, the prime subfield of 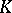 coincides with the field of fractions of the ring
coincides with the field of fractions of the ring 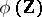 and is isomorphic to the field
and is isomorphic to the field 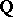 . If
. If 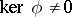 , then
, then 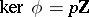 for a certain prime
for a certain prime 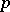 . This
. This 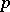 is called the characteristic of the field
is called the characteristic of the field 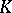 . The prime subfield of
. The prime subfield of 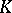 coincides in that case with
coincides in that case with 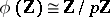 .
.
If 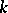 is a subfield of a field
is a subfield of a field 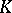 ,
, 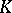 is called an extension of the field
is called an extension of the field 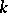 . Let
. Let 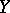 be some subset in
be some subset in 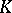 . Then the field
. Then the field 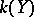 is defined as the smallest subfield of
is defined as the smallest subfield of 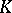 that contains
that contains 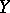 and
and 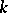 . It is said that
. It is said that 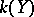 is obtained from
is obtained from 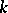 by adjoining the elements from the set
by adjoining the elements from the set 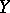 .
.
Basic problems in the theory of fields consist of giving a description of all subfields of a given field, of all fields containing a given field, i.e. overfields (see Extension of a field), to examine all imbeddings of a field in some other field, to classify fields up to an isomorphism, and to examine the automorphism group of a given field.
A field 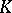 is said to be finitely generated over a subfield
is said to be finitely generated over a subfield 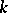 if there exists a finite set
if there exists a finite set 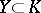 such that
such that 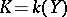 . Any such field can be interpreted as the field of rational functions,
. Any such field can be interpreted as the field of rational functions, 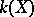 , of a certain irreducible algebraic variety
, of a certain irreducible algebraic variety 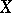 defined over
defined over 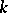 . Algebraic geometry deals, among other things, with the study of such fields. In particular, the classification of such fields is equivalent to the birational classification of irreducible algebraic varieties, and the problem of finding the group of automorphisms of a field
. Algebraic geometry deals, among other things, with the study of such fields. In particular, the classification of such fields is equivalent to the birational classification of irreducible algebraic varieties, and the problem of finding the group of automorphisms of a field 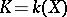 that leave all elements of the field
that leave all elements of the field 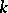 invariant is equivalent to finding all birational automorphisms of the variety
invariant is equivalent to finding all birational automorphisms of the variety 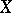 defined over
defined over 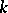 .
.
Galois theory deals with finite separable extensions (cf. Separable extension) of arbitrary fields. An important part in number theory is played by the finite extensions of the field 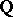 , which are called algebraic number fields. Algebraic number theory deals with these fields.
, which are called algebraic number fields. Algebraic number theory deals with these fields.
Field theory also deals with fields having certain additional structures, such as differential fields, topological fields, ordered fields, formally real and formally 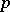 -adic fields, etc.
-adic fields, etc.
Field theory originated (within the framework of the theory of algebraic equations) in the middle of the 19th century. Papers by E. Galois and J.L. Lagrange on group theory and by C.F. Gauss on number theory made it clear that one had to examine the nature of number systems themselves. The concept of a field was put forward in papers by L. Kronecker and R. Dedekind. Dedekind introduced the concept of a field, which he originally called a "rational domainrational domain" . Dedekind's theory was published in the comments and supplements to P.G. Lejeune-Dirichlet's Zahlentheorie. In them, Dedekind substantially supplemented and extended the theory of numbers, the theory of ideals and the theory of finite fields. The term "field" first appeared in the edition of this book in 1871.
References
| [1] | N. Bourbaki, "Eléments de mathematique. Algèbre" , Masson (1981) pp. Chapt. 4–7 |
| [2] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [3] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [4] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
Comments
The German term for "field" is "Körper" and this is of course the term used in [a2]. The edition cited here as [a2] is a corrected reprint of the 4th edition (Braunschweig, 1893); the 1871 edition was the second.
References
| [a1] | N. Jacobson, "Lectures in abstract algebra" , 1. Basic concepts , Springer (1975) |
| [a2] | P.G. Lejeune-Dirichlet, "Zahlentheorie" , Chelsea, reprint (1968) |
Field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Field&oldid=17014