Least-number operator

-operator, minimization operator

A device for constructing new functions out of others, as follows. Let be an 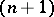-ary arithmetic function, i.e. a function with arguments and values in the set of natural numbers. It is assumed here that is a partial function, i.e. it is not necessarily defined for all values of its arguments. One says that the -ary arithmetic function is obtained from by the least-number operator if, for any natural numbers ,

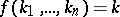if and only if the values of are defined and are not equal to zero for all 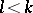, while 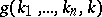is defined and equals zero. If 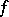is obtained from 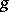by the least-number operator, one writes

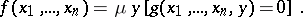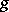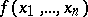An important property of the least-number operator is the following: If is a computable function, then the above function is always partially computable. In fact, if there is an algorithm computing , then the value of can be computed as follows. Compute 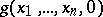. If the computation process ends, i.e. if 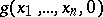is defined, and if 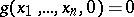, put 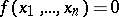; but if 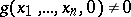, begin to compute 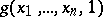. If the process ends and 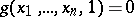, put 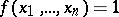; but if 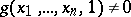, proceed to compute 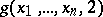; etc. The computation will come to an end if there exists a 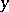such that, for all 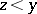, 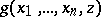is defined and not zero, while 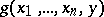is defined and equal to zero. Then .

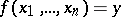The least-number operator plays an important role in the definition of the class of partial recursive functions (cf. Partial recursive function).

References

[a1]	H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165