Kernel of a set
From Encyclopedia of Mathematics
open kernel of a set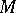 
The set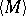 
of all interior points of 
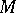. If 
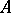and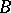 
are mutually complementary sets in a topological space 
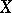, that is, if 
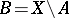, then 
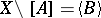and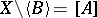 
, where 
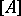denotes the closure of 
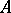(cf. Closure of a set).
Comments
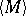is usually called the interior of 
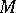(cf. Interior of a set), and is also denoted by 
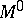and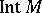 
. The word "kernel" is seldom used in the English mathematical literature in this context.
How to Cite This Entry:
Kernel of a set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_of_a_set&oldid=16955
Kernel of a set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_of_a_set&oldid=16955
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article