Polar decomposition
A polar decomposition of a linear transformation on a finite-dimensional Euclidean (or unitary) space 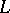 is a decomposition of the linear transformation into a product of a self-adjoint and an orthogonal (respectively, unitary) transformation (cf. Orthogonal transformation; Self-adjoint linear transformation; Unitary transformation). Any linear transformation
is a decomposition of the linear transformation into a product of a self-adjoint and an orthogonal (respectively, unitary) transformation (cf. Orthogonal transformation; Self-adjoint linear transformation; Unitary transformation). Any linear transformation 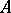 on
on 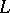 has a polar decomposition
has a polar decomposition
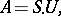 |
where 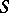 is a positive semi-definite self-adjoint linear transformation and
is a positive semi-definite self-adjoint linear transformation and 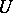 is an orthogonal (or unitary) linear transformation; moreover,
is an orthogonal (or unitary) linear transformation; moreover, 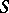 is uniquely defined. If
is uniquely defined. If 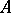 is non-degenerate, then
is non-degenerate, then 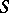 is even positive definite and
is even positive definite and  is also uniquely defined. A polar decomposition on a one-dimensional unitary space coincides with the trigonometric representation of a complex number
is also uniquely defined. A polar decomposition on a one-dimensional unitary space coincides with the trigonometric representation of a complex number  as
as 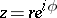 .
.
A.L. Onishchik
A polar decomposition of an operator  acting on a Hilbert space is a representation of
acting on a Hilbert space is a representation of 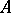 in the form
in the form
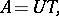 |
where 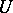 is a partial isometric operator and
is a partial isometric operator and 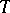 is a positive operator. Any closed operator
is a positive operator. Any closed operator 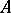 has a polar decomposition, moreover,
has a polar decomposition, moreover, 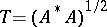 (which is often denoted by
(which is often denoted by  ), and
), and 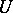 maps the closure
maps the closure 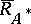 of the domain of the self-adjoint operator
of the domain of the self-adjoint operator 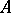 into the closure
into the closure 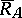 of the range of
of the range of 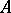 (the von Neumann theorem, see ). A polar decomposition becomes unique if the source and target subspaces of
(the von Neumann theorem, see ). A polar decomposition becomes unique if the source and target subspaces of 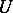 are required to coincide with
are required to coincide with  and
and 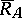 , respectively. On the other hand,
, respectively. On the other hand, 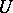 can be always chosen unitary, isometric or co-isometric, depending on the relation between the codimensions of the subspaces
can be always chosen unitary, isometric or co-isometric, depending on the relation between the codimensions of the subspaces 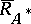 and
and 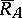 . In particular, if
. In particular, if
 |
then 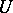 can be chosen unitary and there is a Hermitian operator
can be chosen unitary and there is a Hermitian operator 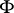 such that
such that  . Then the polar decomposition of
. Then the polar decomposition of 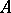 takes the form
takes the form
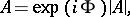 |
entirely analogous to the polar decomposition of a complex number. Commutativity of the terms in a polar decomposition takes place if and only if the operator is normal (cf. Normal operator).
An expression analogous to the polar decomposition has been obtained for operators on a space with an indefinite metric (see , ).
A polar decomposition of a functional on a von Neumann algebra 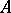 is a representation of a normal functional
is a representation of a normal functional 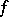 on
on 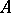 in the form
in the form 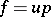 , where
, where 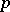 is a positive normal functional on
is a positive normal functional on 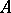 ,
, 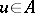 is a partial isometry (i.e.
is a partial isometry (i.e. 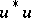 and
and 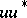 are projectors), and multiplication is understood as the action on
are projectors), and multiplication is understood as the action on 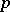 of the operator which is adjoint to left multiplication by
of the operator which is adjoint to left multiplication by  in
in 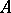 :
: 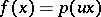 for all
for all 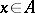 . A polar decomposition can always be realized so that the condition
. A polar decomposition can always be realized so that the condition 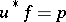 is fulfilled. Under this condition a polar decomposition is unique.
is fulfilled. Under this condition a polar decomposition is unique.
Any bounded linear functional 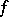 on an arbitrary
on an arbitrary 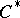 -algebra
-algebra 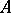 can be considered as a normal functional on the universal enveloping von Neumann algebra
can be considered as a normal functional on the universal enveloping von Neumann algebra 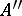 ; the corresponding polar decomposition
; the corresponding polar decomposition 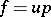 is called the enveloping polar decomposition of the functional
is called the enveloping polar decomposition of the functional  . The restriction of the functional
. The restriction of the functional 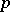 to
to 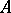 is called the absolute value of
is called the absolute value of 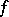 and is denoted by
and is denoted by 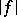 ; the following properties determine the functional
; the following properties determine the functional  uniquely:
uniquely:
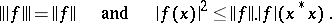 |
In the case when 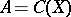 is the algebra of all continuous functions on a compactum, the absolute value of a functional corresponds to the total variation of the measure determined by it (cf. also Total variation of a function).
is the algebra of all continuous functions on a compactum, the absolute value of a functional corresponds to the total variation of the measure determined by it (cf. also Total variation of a function).
In many cases a polar decomposition of a functional allows one to reduce studies of functionals on 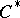 -algebras to studies of positive functionals. It enables one, for example, to construct for each
-algebras to studies of positive functionals. It enables one, for example, to construct for each 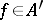 a representation
a representation 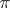 of the algebra
of the algebra  on which
on which 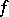 has a vector realization (i.e. there are vectors
has a vector realization (i.e. there are vectors 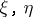 in
in 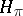 such that
such that 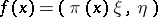 ,
, 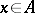 ). The representation
). The representation 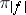 constructed from the positive functional
constructed from the positive functional 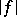 using the GNS-construction (of Gel'fand–Naimark–Segal) has that property.
using the GNS-construction (of Gel'fand–Naimark–Segal) has that property.
The polar decomposition of an element of a 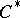 -algebra is a representation of the element as the product of a positive element and a partial isometric element. Polar decomposition is not valid for all elements: in the usual polar decomposition of an operator
-algebra is a representation of the element as the product of a positive element and a partial isometric element. Polar decomposition is not valid for all elements: in the usual polar decomposition of an operator 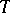 on a Hilbert space the positive term belongs to the
on a Hilbert space the positive term belongs to the 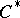 -algebra generated by
-algebra generated by 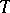 , but for the partial isometric term one can only state that it belongs to the von Neumann algebra generated by
, but for the partial isometric term one can only state that it belongs to the von Neumann algebra generated by 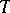 . That is why one defines and uses the so-called enveloping polar decomposition of an element
. That is why one defines and uses the so-called enveloping polar decomposition of an element 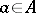 :
: 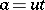 , where
, where  and
and  is a partial isometric element in the universal enveloping von Neumann algebra
is a partial isometric element in the universal enveloping von Neumann algebra 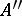 (it is assumed that
(it is assumed that 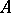 is canonically imbedded in
is canonically imbedded in 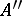 ).
).
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [2] | J. Bognár, "Certain relations among the non-negativity properties of operators on spaces with an indefinite metric II" Stud. Scient. Math. Hung. , 1 : 1–2 (1966) pp. 97–102 (In Russian) |
| [3] | J. Dixmier, "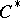 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
V.S. Shul'man
Comments
References
| [a1] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , Transl. Math. Monogr. , 18 , Amer. Math. Soc. (1969) (Translated from Russian) |
Polar decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polar_decomposition&oldid=16949