Etale morphism

A smooth morphism of algebraic varieties or schemes of relative dimension . An étale morphism of schemes can be defined equivalently as a locally finitely-presentable flat morphism such that for any point 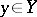the -scheme 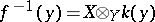is finite and separable. An étale morphism has the lifting property for infinitesimal deformations: If is an étale morphism, is an affine 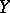-scheme and is a closed subscheme of given by a nilpotent sheaf of ideals, then the natural mapping 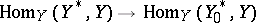is bijective. This property characterizes the étale morphisms. Finally, an étale morphism can be defined as being flat and unramified. (A locally finitely-presentable morphism 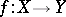is unramified if the diagonal imbedding 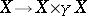is a local isomorphism.)

Being étale (like being smooth and being unramified) is preserved under composition of morphism and under base change. An open imbedding is an étale morphism. Any morphism between étale 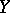-schemes is étale. For smooth varieties the fact that 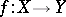is étale means that 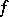induces an isomorphism of the tangent spaces. Locally, an étale morphism is given by a polynomial with non-zero derivative.

Etale morphisms play an important role in étale cohomology theory (cf. Etale cohomology) in the definitions of the fundamental group of a scheme, of an algebraic space and of a Hensel ring.

References

[1]	A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" Publ. Math. IHES , 32 (1967)
[2]	A. Grothendieck (ed.) et al. (ed.) , Revêtements étales et groupe fondamental. SGA 1 , Lect. notes in math. , 224 , Springer (1971)

References

[a1]	A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique: Etude locale des schémas et de morphismes de schémas" Publ. Math. IHES , 4 (1965) pp. Part 4, Sect. 17.6