Branch point

singular point of multi-valued character

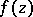An isolated singular point of an analytic function of one complex variable such that the analytic continuation of an arbitrary function element of 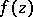along a closed path which encircles yields new elements of 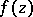. More exactly, is said to be a branch point if there exist: 1) an annulus 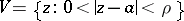in which 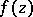can be analytically extended along any path; 2) a point and some function element of 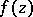represented by a power series

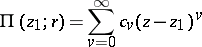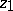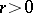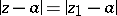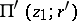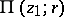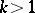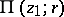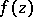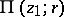with centre and radius of convergence , the analytic continuation of which along the circle , going around the path once in, say, the positive direction, yields a new element different from . If, after a minimum number of such rounds the initial element is again obtained, this is also true of all elements of the branch (cf. Branch of an analytic function) of defined in by the element . In such a case is a branch point of finite order 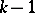of this branch. In a punctured neighbourhood 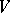of a branch point of finite order this branch is represented by a generalized Laurent series, or Puiseux series:

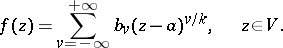(1)

If 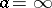is an improper branch point of a finite order, then the branch of 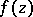is representable in some neighbourhood 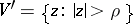by an analogue of the series (1):

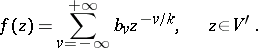(2)

The behaviour of the Riemann surface 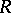of 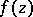over a branch point of finite order is characterized by the fact that 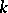sheets of the branch of 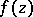defined by the element 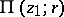come together over . At the same time the behaviour of other branches of 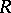over may be altogether different.

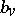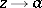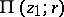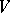If the series (1) or (2) contains only a finite number of non-zero coefficients with negative indices , is an algebraic branch point or an algebraic singular point. Such a branch point of finite order is also characterized by the fact that as in whatever manner, the values of all elements of the branch defined by in or 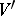tend to a definite finite or infinite limit.

Example: 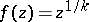, where 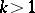is a natural number, .

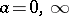If the series (1) or (2) contain an infinite number of non-zero coefficients 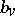with negative indices , the branch points of finite order belong the class of transcendental branch points.

Example: 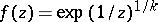, where 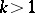is a natural number, .

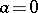Finally, if it is impossible to return to the initial element after a finite number of turns, is said to be a logarithmic branch point or a branch point of infinite order, and is also a transcendental branch point.

Example: .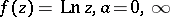

Infinitely many sheets of the branch of 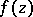defined by the element 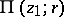come together over a logarithmic branch point.

In the case of an analytic function of several complex variables 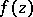, , 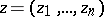, 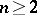a point of the space 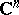or 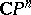is said to be a branch point of order 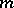, , 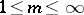if it is a branch point of order 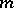of the, generally many-sheeted, domain of holomorphy of 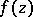. Unlike in the case 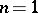, branch points, just like other singular points of analytic functions (cf. Singular point), cannot be isolated if .

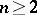References

[1]	A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) pp. Chapt. 8 (Translated from Russian)
[2]	B.A. Fuks, "Theory of analytic functions of several complex variables" , Amer. Math. Soc. (1963) (Translated from Russian)