Heinz-Kato-Furuta inequality

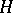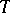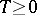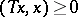In the sequel, a capital letter denotes a bounded linear operator on a Hilbert space . An operator is said to be positive (denoted by ) if for all .

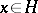The following Heinz–Kato–Furuta inequality can be considered as an extension of the Heinz–Kato inequality, since for the Heinz–Kato inequality is obtained from the Heinz–Kato–Furuta inequality.

The Heinz–Kato–Furuta inequality (1994; cf. [a2]): If 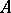and 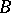are positive operators such that 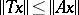and 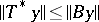for all 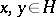, then for all :

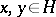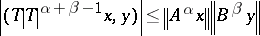(a1)

for all 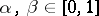such that .

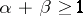As generalizations of the Heinz–Kato–Furuta inequality, two determinant-type generalizations, expressed in terms of 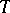, 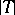and 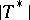, can be obtained by using the Furuta inequality. It turns out that each of these two generalizations is equivalent to the Furuta inequality. Results similar to these determinant-type generalizations but under the conditions 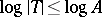and 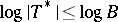, which are weaker than the original conditions 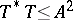and 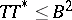in the Heinz–Kato inequality, have also been obtained. A nice application of the Heinz–Kato–Furuta inequality is given in [a1].

Additional references can be found in Heinz inequality.

References

[a1]	M. Fujii, S. Izumino, R. Nakamoto, "Classes of operators determined by the Heinz–Kato–Furuta inequality and the Hölder–MacCarthy inequality" Nihonkai Math. J. , 5 (1994) pp. 61–67
[a2]	T. Furuta, "An extension of the Heinz–Kato theorem" Proc. Amer. Math. Soc. , 120 (1994) pp. 785–787