Symmetric operator
A linear mapping 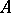 of a set
of a set 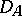 in a Hilbert space
in a Hilbert space 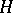 (in general, complex) into
(in general, complex) into 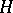 such that
such that 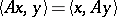 for all
for all 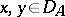 . If
. If 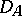 is an everywhere-dense linear manifold in
is an everywhere-dense linear manifold in 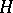 (and this is assumed in what follows), then
(and this is assumed in what follows), then 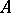 is a linear operator. If
is a linear operator. If 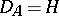 , then
, then  is bounded and hence continuous on
is bounded and hence continuous on 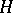 . A symmetric operator
. A symmetric operator 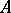 induces a bilinear Hermitian form
induces a bilinear Hermitian form 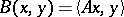 on
on 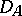 , that is,
, that is, 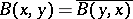 . The corresponding quadratic form
. The corresponding quadratic form 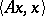 is real. Conversely, if the form
is real. Conversely, if the form 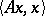 on
on 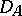 is real, then
is real, then 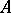 is symmetric. The sum
is symmetric. The sum 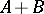 of two symmetric operators
of two symmetric operators 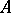 and
and 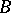 with a common domain of definition
with a common domain of definition 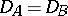 is again a symmetric operator, while if
is again a symmetric operator, while if 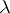 is a real number, then
is a real number, then 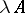 is also symmetric. Every symmetric operator
is also symmetric. Every symmetric operator 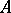 has a uniquely defined closure
has a uniquely defined closure 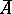 and an adjoint
and an adjoint 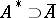 . In general,
. In general, 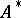 is not symmetric and
is not symmetric and 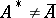 . If
. If 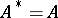 , then
, then 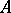 is called a self-adjoint operator. This holds, for example, in the case of symmetric operators defined on the whole of
is called a self-adjoint operator. This holds, for example, in the case of symmetric operators defined on the whole of 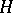 . If
. If 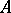 is symmetric and bounded on
is symmetric and bounded on 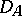 , then
, then 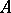 can be extended as a bounded symmetric operator to the whole of
can be extended as a bounded symmetric operator to the whole of 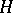 .
.
Examples.
1) Let 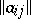 ,
, 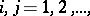 be an infinite matrix such that
be an infinite matrix such that 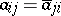 , and
, and
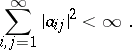 |
Then the system of equations
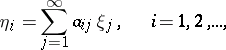 |
defining 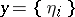 for an
for an 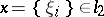 , defines a bounded symmetric operator, which turns out to be self-adjoint on the complex space
, defines a bounded symmetric operator, which turns out to be self-adjoint on the complex space 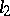 .
.
2) In the complex space 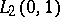 , let
, let 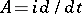 be defined on the set
be defined on the set 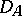 of absolutely-continuous functions
of absolutely-continuous functions  on
on 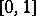 having a square-summable derivative and satisfying the condition
having a square-summable derivative and satisfying the condition 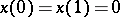 . Then
. Then 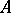 is symmetric but not self-adjoint.
is symmetric but not self-adjoint.
References
| [1] | L.A. [L.A. Lyusternik] Liusternik, "Elements of functional analysis" , F. Ungar (1961) (Translated from Russian) |
| [2] | F. Riesz, B. Szökevalfi-Nagy, "Leçons d'analyse fonctionelle" , Akad. Kiado (1955) |
Comments
An important problem is to find a self-adjoint extension of a symmetric operator. This problem has different versions, depending on whether one looks for an extension in the original or in a larger space. A complete theory of this topic exists.
References
| [a1] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1980) (Translated from Russian) |
Symmetric operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_operator&oldid=16902