Bloch constant

An absolute constant, the existence of which is established by Bloch's theorem. Let 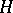be the class of all holomorphic functions 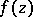in the disc 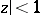such that 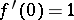. The Riemann surface of the function 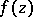contains on one of its sheets a largest open disc of radius 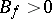. It was shown by A. Bloch [1] that

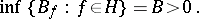The most precise known estimate is 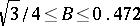[2]. It follows from Bloch's theorem that the Riemann surface of an entire function contains single-sheeted discs of arbitrary radius; this is equivalent to the Picard theorem.

References

[1]	A. Bloch, "Les théorèmes de M. Valiron sur les fonctions entières et la théorie de l'uniformisation" Ann. Fac. Sci. Univ. Toulouse (3) , 17 (1925) pp. 1–22
[2]	L.V. Ahlfors, H. Grunsky, "Ueber die Blochsche Konstante" Math. Z. , 42 (1937) pp. 671–673
[3]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)

Comments

For the connection between the theorems of Bloch and Picard, see e.g. [a1].

References

[a1]	M. Heins, "Selected topics in the classical theory of functions of a complex variable" , Holt, Rinehart & Winston (1962)