Isometric operator

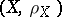A mapping of a metric space into a metric space such that

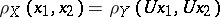for all 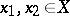. If and are real normed linear spaces, and 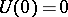, then 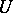is a linear operator.

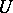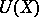An isometric operator maps one-to-one onto , so that the inverse operator 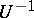exists, and this is also an isometric operator. The conjugate of a linear isometric operator from some normed linear space into another is also isometric. A linear isometric operator mapping 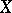onto the whole of 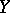is said to be a unitary operator. The condition for a linear operator 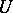acting on a Hilbert space 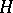to be unitary is the equation 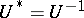. The spectrum of a unitary operator (cf. Spectrum of an operator) lies on the unit circle, and 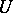has a representation

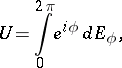where 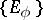is the corresponding resolution of the identity. An isometric operator defined on a subspace of a Hilbert space and taking values in that space can be extended to a unitary operator if the orthogonal complement of its domain of definition and its range have the same dimension.

With every symmetric operator 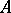with domain of definition 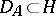is associated the isometric operator

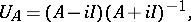called the Cayley transform o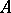f . If 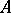is self-adjoint, then 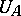is unitary.

Two operators 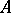and 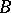with the same domain of definition 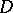are said to be metrically equal if 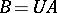, where 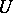is an isometric operator, that is, if 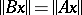for all 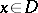. Such operators have a number of properties in common. For every bounded linear operator 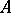acting on a Hilbert space there exists one and only one positive operator metrically equal to it, namely that defined by the equality .

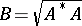References

[1]	N.I. Akhiezer, I.M. Glazman, "Theory of linear operators on a Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian)
[2]	A.I. Plesner, "Spectral theory of linear operators" , F. Ungar (1965) (Translated from Russian)
[3]	B. Mazur, S. Ulam, "Sur les transformations isométriques d'espaces vectoriels normés" C.R. Acad. Sci. Paris , 194 (1932) pp. 946–948