Irreducible mapping
A continuous mapping of a topological space 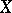 onto a topological space
onto a topological space 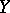 such that the image of every closed set in
such that the image of every closed set in 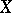 , other than
, other than  itself, is different from
itself, is different from 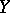 . If
. If 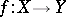 is a continuous mapping,
is a continuous mapping, 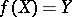 , and if all inverse images of points under
, and if all inverse images of points under 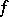 are compact, then there exists a closed subspace
are compact, then there exists a closed subspace 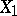 in
in 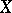 such that
such that 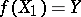 and such that the restriction of
and such that the restriction of 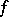 to
to  is an irreducible mapping. The combination of the requirements on a mapping of being irreducible and being closed has an outstanding effect: Spaces linked by such mappings do not differ in a number of important characteristics; in particular, they have the same Suslin number and
is an irreducible mapping. The combination of the requirements on a mapping of being irreducible and being closed has an outstanding effect: Spaces linked by such mappings do not differ in a number of important characteristics; in particular, they have the same Suslin number and 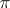 -weight. But the main value of closed irreducible mappings lies in the central role they play in the theory of absolutes.
-weight. But the main value of closed irreducible mappings lies in the central role they play in the theory of absolutes.
References
| [1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
Comments
See Absolute.
References
| [a1] | J.R. Porter, R.G. Woods, "Extensions and absolutes of Hausdorff spaces" , Springer (1988) |
Irreducible mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irreducible_mapping&oldid=16891