Cross product
crossed product, of a group  and a ring
and a ring 
An associative ring defined as follows. Suppose one is given a mapping  of a group
of a group  into the isomorphism group of an associative ring
into the isomorphism group of an associative ring  with an identity, and a family
with an identity, and a family
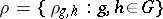 |
of invertible elements of  , satisfying the conditions
, satisfying the conditions
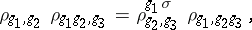 |
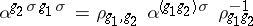 |
for all 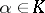 and
and 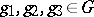 . The family
. The family  is called a factor system. Then the cross product of
is called a factor system. Then the cross product of 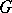 and
and  with respect to the factor system
with respect to the factor system  and the mapping
and the mapping  is the set of all formal finite sums of the form
is the set of all formal finite sums of the form
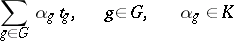 |
(where the  are symbols uniquely assigned to every element
are symbols uniquely assigned to every element  ), with binary operations defined by
), with binary operations defined by
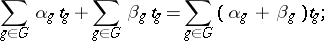 |
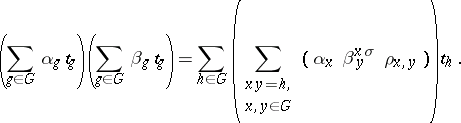 |
This ring is denoted by  ; the elements
; the elements  form a
form a 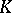 -basis of it.
-basis of it.
If  maps
maps 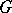 onto the identity automorphism of
onto the identity automorphism of  , then
, then 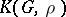 is called a twisted or crossed group ring, and if, in addition,
is called a twisted or crossed group ring, and if, in addition,  for all
for all  , then
, then 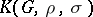 is the group ring of
is the group ring of 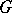 over
over 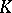 (see Group algebra).
(see Group algebra).
Let  be a field and
be a field and  a monomorphism. Then
a monomorphism. Then 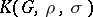 is a simple ring, being the cross product of the field with its Galois group.
is a simple ring, being the cross product of the field with its Galois group.
References
| [1] | S.K. Sehgal, "Topics in group rings" , M. Dekker (1978) |
| [2] | A.A. Bovdi, "Cross products of semi-groups and rings" Sibirsk. Mat. Zh. , 4 (1963) pp. 481–499 (In Russian) |
| [3] | A.E. Zalesskii, A.V. Mikhalev, "Group rings" J. Soviet Math. , 4 (1975) pp. 1–74 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 2 (1973) pp. 5–118 |
| [4] | D.S. Passman, "The algebraic structure of group rings" , Wiley (1977) |
Comments
In the defining relations for a factor system above  , e.g., of course stands for the result of applying the automorphism
, e.g., of course stands for the result of applying the automorphism  to the element
to the element  . If
. If  for all
for all  , then one obtains the skew group ring
, then one obtains the skew group ring  . Cross products arise naturally when dealing with extensions. Indeed, let
. Cross products arise naturally when dealing with extensions. Indeed, let  be a normal subgroup of
be a normal subgroup of 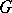 . Choose a set of representatives
. Choose a set of representatives  of
of  in
in  . Then every
. Then every 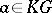 , the group algebra of
, the group algebra of 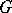 , can be written as a unique sum
, can be written as a unique sum  ,
, 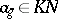 . Now write
. Now write
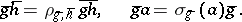 |
Then the  define a factor system (for the group
define a factor system (for the group 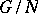 and the ring
and the ring  relative to the set of automorphisms
relative to the set of automorphisms  ) and
) and
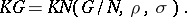 |
Up to Brauer equivalence every central simple algebra is a cross product, but not every division algebra is isomorphic to a cross product. Two algebras  over
over  are Brauer equivalent if
are Brauer equivalent if 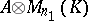 is isomorphic to
is isomorphic to  for suitable
for suitable 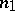 and
and  . Here
. Here 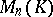 is the algebra of
is the algebra of 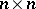 matrices over
matrices over  . Cf. also Brauer group.
. Cf. also Brauer group.
Cross product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cross_product&oldid=16831