Length
A numerical characteristic of the extension of lines in a metric space. The length of a segment of a straight line is the distance between its ends, measured by means of some segment accepted as the unit length. The length of a broken line is the sum of the lengths of its parts. The length of a simple arc is the least upper bound of the lengths of the broken lines inscribed in this arc. Any continuous curve has a length, finite or infinite. If its length is finite, the curve is known as rectifiable. The length of a planar curve defined in rectangular coordinates by an equation 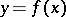 ,
, 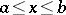 (
(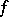 having a continuous derivative
having a continuous derivative 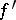 ) is given by the integral
) is given by the integral
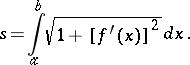 |
If the curve is given in parametric form
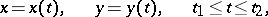 |
its length is given by
 |
The length of a rectifiable curve does not depend on the parametrization. The length of a spatial curve given in parametric form 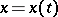 ,
, 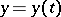 ,
, 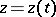 ,
, 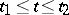 , is given by the formula
, is given by the formula
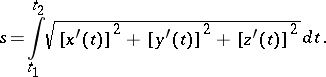 |
In the case of an  -dimensional space,
-dimensional space,
 |
Let 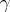 be a continuously-differentiable curve, given by functions
be a continuously-differentiable curve, given by functions  ,
, 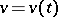 , on a continuously-differentiable surface
, on a continuously-differentiable surface 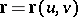 . Then the length of an arc of the curve counted from the point corresponding to the parameter value
. Then the length of an arc of the curve counted from the point corresponding to the parameter value  is equal to
is equal to
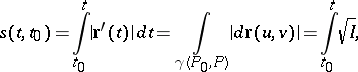 |
where 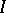 is the first fundamental form of the surface. The length of a continuously-differentiable curve given by functions
is the first fundamental form of the surface. The length of a continuously-differentiable curve given by functions 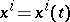 ,
, 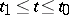 , in a Riemannian space with metric tensor
, in a Riemannian space with metric tensor  is
is
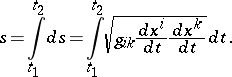 |
Comments
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a2] | L. Blumenthal, K. Menger, "Studies in geometry" , Freeman (1970) |
| [a3] | H. Busemann, "The geometry of geodesics" , Acad. Press (1955) |
Length. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Length&oldid=16816