Determinant variety
The set of matrices 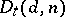 of dimension
of dimension  and of a rank lower than
and of a rank lower than 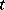 , with the structure of an algebraic variety. Let
, with the structure of an algebraic variety. Let  be the ideal in the ring of polynomials
be the ideal in the ring of polynomials
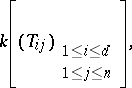 |
with coefficients in a field  , generated by the
, generated by the 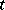 -order minors of the matrix of dimension
-order minors of the matrix of dimension  constituted by the variables
constituted by the variables  (a determinant ideal). The set of zeros of the ideal
(a determinant ideal). The set of zeros of the ideal  in the affine space
in the affine space 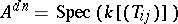 is known as the determinant variety and is denoted by
is known as the determinant variety and is denoted by 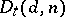 . For any commutative
. For any commutative  -algebra
-algebra 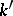 the set of
the set of 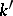 -points of the determinant variety
-points of the determinant variety 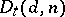 coincides, in a natural manner, with the set of matrices of dimension
coincides, in a natural manner, with the set of matrices of dimension  and rank
and rank  with coefficients in
with coefficients in  .
.
The following are special cases of determinant varieties: 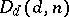 is the hypersurface in
is the hypersurface in  defined by the vanishing of the determinant of a square matrix of dimension
defined by the vanishing of the determinant of a square matrix of dimension 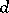 consisting of independent variables (a determinant hypersurface);
consisting of independent variables (a determinant hypersurface);  is an affine cone for the image of the Segre imbedding
is an affine cone for the image of the Segre imbedding
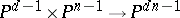 |
of the product of projective spaces [2].
Determinant varieties have the following properties: 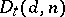 is irreducible, reduced (i.e. the ideal
is irreducible, reduced (i.e. the ideal  is simple), is a Cohen–Macaulay variety (cf. Cohen–Macaulay ring), is normal, and the dimension of
is simple), is a Cohen–Macaulay variety (cf. Cohen–Macaulay ring), is normal, and the dimension of 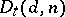 is equal to
is equal to  [1], [2].
[1], [2]. 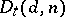 is a Gorenstein scheme if and only if
is a Gorenstein scheme if and only if 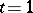 or
or 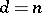 (cf. Gorenstein ring) [5]. Determinant varieties are closely connected with Schubert varieties of a Grassmann manifold (cf. Schubert variety).
(cf. Gorenstein ring) [5]. Determinant varieties are closely connected with Schubert varieties of a Grassmann manifold (cf. Schubert variety).
References
| [1] | M. Hochster, J. Eagon, "Cohen–Macaulay rings, invariant theory, and the generic perfection of determinantal loci" Amer. J. Math. , 93 : 4 (1971) pp. 1020–1058 |
| [2] | S. Kleiman, J. Landolfi, "Geometry and deformation of special Schubert varieties" Compositio Math. , 23 (1971) pp. 407–434 |
| [3] | D. Laksov, "Deformation of determinantal schemes" Compositio Math. , 30 (1975) pp. 273–292 |
| [4] | C. Musili, "Some properties of Schubert varieties" J. Indian Math. Soc. , 38 (1974) pp. 131–145 |
| [5] | T. Svanes, "Coherent cohomology on Schubert subschemes of flag schemes and applications" Adv. in Math. , 14 (1974) pp. 369–453 |
Comments
Many geometrical properties of determinant varieties can be found in [a1]. Instead of determinant variety, etc. one also speaks of determinantal variety, etc.
References
| [a1] | T.G. Room, "Geometry of determinantal loci" , Cambridge Univ. Press (1938) |
Determinant variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Determinant_variety&oldid=16799