Conformal mapping, boundary properties of a
Properties of functions mapping one domain in the complex plane conformally onto another that show up near the boundary of the mapped domain and on the boundary itself. Among such properties are: the possibility of continuously extending a function 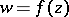 mapping a given domain
mapping a given domain 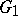 conformally onto a domain
conformally onto a domain  to some point
to some point 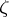 of the boundary
of the boundary  of
of 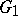 or to the entire boundary
or to the entire boundary  of this domain; the nature of the discontinuity in the case where such an extension is not possible; conformality of the extended mapping at the boundary points
of this domain; the nature of the discontinuity in the case where such an extension is not possible; conformality of the extended mapping at the boundary points  ; the differentiability or smoothness properties of the extended function on
; the differentiability or smoothness properties of the extended function on 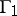 and on the closed domain
and on the closed domain 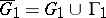 ; or the membership of the derivative of the mapping function to various classes of analytic functions in
; or the membership of the derivative of the mapping function to various classes of analytic functions in 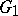 , etc. These properties are studied in their dependence on the properties of the boundaries of
, etc. These properties are studied in their dependence on the properties of the boundaries of 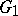 and
and 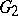 . From among the most general boundary properties of conformal mappings one can distinguish: For any simply-connected domains
. From among the most general boundary properties of conformal mappings one can distinguish: For any simply-connected domains 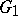 and
and 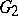 and any univalent conformal mapping
and any univalent conformal mapping 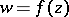 of
of 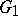 onto
onto 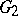 , this mapping sets up a one-to-one correspondence between the prime ends (cf. Limit elements) of these domains in the sense that the class of all equivalent paths lying in
, this mapping sets up a one-to-one correspondence between the prime ends (cf. Limit elements) of these domains in the sense that the class of all equivalent paths lying in 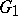 and defining some prime end
and defining some prime end 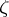 of
of 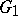 is taken by this mapping into the class of all equivalent paths lying in
is taken by this mapping into the class of all equivalent paths lying in 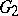 and defining some prime end
and defining some prime end 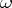 of
of 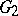 (the inverse mapping
(the inverse mapping 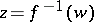 ,
, 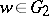 , takes the class of equivalent paths defining
, takes the class of equivalent paths defining 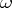 into the class of equivalent paths defining
into the class of equivalent paths defining 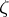 ). Furthermore,
). Furthermore, 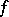 determines, in a special topology, a homeomorphism of the domain
determines, in a special topology, a homeomorphism of the domain  with its prime ends adjoined (regarded together with the points
with its prime ends adjoined (regarded together with the points 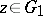 as points of a topological space) onto the domain
as points of a topological space) onto the domain 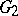 with prime ends adjoined. One usually considers the case when one of the domains
with prime ends adjoined. One usually considers the case when one of the domains 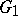 ,
, 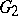 is the unit disc
is the unit disc 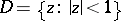 (more rarely, the half-plane or a sector); the general case reduces to this particular case.
(more rarely, the half-plane or a sector); the general case reduces to this particular case.
Let 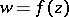 be a univalent conformal mapping of the disc
be a univalent conformal mapping of the disc 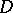 with boundary
with boundary 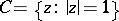 onto a bounded domain
onto a bounded domain 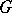 with boundary
with boundary 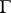 , let
, let 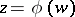 be its inverse:
be its inverse: 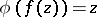 for
for  . Then one has the following results.
. Then one has the following results.
1) In order that  be continuously extendable to a point
be continuously extendable to a point 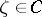 it is necessary and sufficient that the prime end of
it is necessary and sufficient that the prime end of 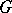 corresponding to
corresponding to 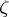 under this mapping be a prime end of the first kind (that is, it consists of a single point). In order that
under this mapping be a prime end of the first kind (that is, it consists of a single point). In order that 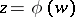 be continuously extendable to a point
be continuously extendable to a point 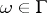 it is necessary and sufficient that
it is necessary and sufficient that 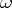 be part of just one prime end (more precisely, be part of just one support of a prime end of
be part of just one prime end (more precisely, be part of just one support of a prime end of 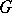 ). If
). If 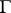 is a closed Jordan curve, then
is a closed Jordan curve, then 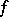 is continuously extendable onto
is continuously extendable onto 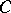 , and
, and 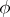 onto
onto 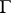 , so that the extended functions realize a one-to-one bicontinuous mapping (a homeomorphism) of the closed domains
, so that the extended functions realize a one-to-one bicontinuous mapping (a homeomorphism) of the closed domains 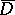 ,
, 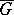 onto each other.
onto each other.
In what follows 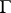 denotes a Jordan curve and it is supposed that the functions
denotes a Jordan curve and it is supposed that the functions 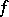 and
and 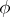 are extended onto
are extended onto 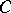 and
and  , respectively.
, respectively.
2) If 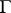 is a closed rectifiable Jordan curve, then the boundary functions
is a closed rectifiable Jordan curve, then the boundary functions 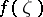 ,
, 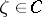 , and
, and 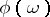 ,
,  , are absolutely continuous. Thus,
, are absolutely continuous. Thus,  ,
, 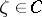 , and
, and 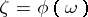 ,
,  , take boundary sets of measure zero to boundary sets of measure zero. The function
, take boundary sets of measure zero to boundary sets of measure zero. The function 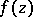 has a finite non-zero derivative relative to the closed disc
has a finite non-zero derivative relative to the closed disc 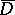 at almost-every point
at almost-every point  , while
, while  has a finite non-zero derivative at almost-every point
has a finite non-zero derivative at almost-every point 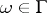 . Consequently, these mappings are conformal (that is, have the property of constant dilation and preservation of angles) at almost-every boundary point of their respective domains. The function
. Consequently, these mappings are conformal (that is, have the property of constant dilation and preservation of angles) at almost-every boundary point of their respective domains. The function 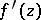 belongs to the Hardy class
belongs to the Hardy class  .
.
3) Let  be a closed rectifiable Jordan curve with the following property: For any distinct points
be a closed rectifiable Jordan curve with the following property: For any distinct points  , the ratio of the length of the smaller of the arcs into which these points divide
, the ratio of the length of the smaller of the arcs into which these points divide 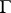 to the distance
to the distance 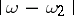 between these points is bounded from above by some quantity
between these points is bounded from above by some quantity 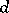 that does not depend on
that does not depend on  or
or 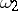 . Then
. Then 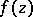 satisfies the Hölder condition of order
satisfies the Hölder condition of order 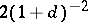 on
on 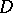 .
.
4) Let 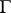 be a smooth closed Jordan curve. A point
be a smooth closed Jordan curve. A point 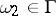 is fixed and for
is fixed and for  an arc of length
an arc of length 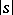 is laid-off along
is laid-off along 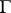 in the positive (when
in the positive (when  ) or negative (when
) or negative (when 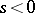 ) direction of traversal of
) direction of traversal of 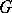 . Let
. Let 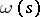 be the end of the arc laid-off, and let
be the end of the arc laid-off, and let 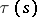 be the angle between the positive direction of the real axis and the positive direction of the tangent at
be the angle between the positive direction of the real axis and the positive direction of the tangent at 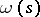 (the value of
(the value of  is chosen so that the function
is chosen so that the function 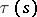 is continuous). If there exists for some
is continuous). If there exists for some 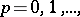 a derivative
a derivative  satisfying a Hölder condition of some positive order
satisfying a Hölder condition of some positive order 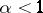 , then the function
, then the function 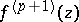 is continuous and satisfies the Hölder condition of the same order
is continuous and satisfies the Hölder condition of the same order 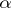 on the closed disc
on the closed disc 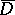 , moreover
, moreover 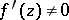 on
on 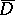 and
and 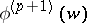 is continuous and satisfies the Hölder condition of order
is continuous and satisfies the Hölder condition of order 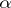 on
on 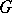 with, moreover,
with, moreover, 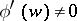 on
on 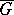 .
.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) (Translated from Russian) |
| [2] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6 |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [5] | S.E. Warschawski, "On differentiability at the boundary in conformal mapping" Proc. Amer. Math. Soc. , 12 : 4 (1961) pp. 614–620 |
| [6] | O.D. Kellogg, "Harmonic functions and Green's integral" Trans. Amer. Math. Soc. , 13 : 1 (1912) pp. 109–132 |
| [7] | E.P. Dolzhenko, "Smoothness of harmonic and analytic functions at boundary points of a domain" Izv. Akad. Nauk SSSR Ser. Mat. , 29 (1965) pp. 1069–1084 (In Russian) |
Conformal mapping, boundary properties of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conformal_mapping,_boundary_properties_of_a&oldid=16790