Reinhardt domain

multiple-circled domain

A domain in the complex space , , with centre at a point , with the following property: Together with any point , the domain also contains the set

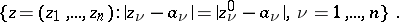A Reinhardt domain with is invariant under the transformations , , 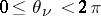. The Reinhardt domains constitute a subclass of the Hartogs domains (cf. Hartogs domain) and a subclass of the circular domains, which are defined by the following condition: Together with any 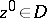, the domain contains the set

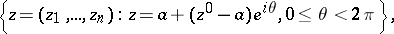i.e. all points of the circle with centre and radius 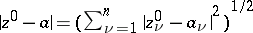that lie on the complex line through and .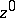

A Reinhardt domain 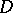is called a complete Reinhardt domain if together with any point 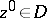it also contains the polydisc

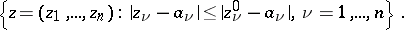A complete Reinhardt domain is star-like with respect to its centre (cf. Star-like domain).

Examples of complete Reinhardt domains are balls and polydiscs in . A circular domain 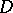is called a complete circular domain if together with any pont it also contains the entire disc .

A Reinhardt domain is called logarithmically convex if the image 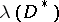of the set

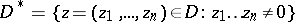under the mapping

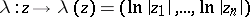is a convex set in the real space . An important property of logarithmically-convex Reinhardt domains is the following: Every such domain in is the interior of the set of points of absolute convergence (i.e. the domain of convergence) of some power series in , and conversely: The domain of convergence of any power series in is a logarithmically-convex Reinhardt domain with centre .

References

[1]	V.S. Vladimirov, "Methods of the theory of functions of many complex variables" , M.I.T. (1966) (Translated from Russian)
[2]	B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian)

Comments

The final paragraph reduces to: A Reinhardt domain is a domain of holomorphy if and only if it is logarithmically convex.

References

[a1]	L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973)
[a2]	R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986)