Witt theorem
Any isometry between two subspaces  and
and  of a finite-dimensional vector space
of a finite-dimensional vector space  , defined over a field
, defined over a field  of characteristic different from 2 and provided with a metric structure induced from a non-degenerate symmetric or skew-symmetric bilinear form
of characteristic different from 2 and provided with a metric structure induced from a non-degenerate symmetric or skew-symmetric bilinear form  , may be extended to a metric automorphism of the entire space
, may be extended to a metric automorphism of the entire space  . The theorem was first obtained by E. Witt [1].
. The theorem was first obtained by E. Witt [1].
Witt's theorem may also be proved under wider assumptions on  and
and  [2], [3]. In fact, the theorem remains valid if
[2], [3]. In fact, the theorem remains valid if  is a skew-field,
is a skew-field, 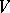 is a finite-dimensional left
is a finite-dimensional left 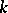 -module and
-module and 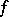 is a non-degenerate
is a non-degenerate  -Hermitian form (with respect to some fixed involutory anti-automorphism
-Hermitian form (with respect to some fixed involutory anti-automorphism  of
of 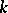 , cf. Hermitian form) satisfying the following condition: For any
, cf. Hermitian form) satisfying the following condition: For any 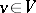 there exists an element
there exists an element 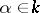 such that
such that
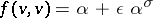 |
(property  ). Property
). Property 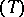 holds if, for example,
holds if, for example, 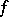 is a Hermitian form and the characteristic of
is a Hermitian form and the characteristic of 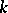 is different from 2, or if
is different from 2, or if 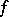 is an alternating form. Witt's theorem is also valid if
is an alternating form. Witt's theorem is also valid if 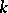 is a field and
is a field and 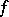 is the symmetric bilinear form associated with a non-degenerate quadratic form
is the symmetric bilinear form associated with a non-degenerate quadratic form 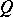 on
on 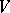 . It follows from Witt's theorem that the group of metric automorphisms of
. It follows from Witt's theorem that the group of metric automorphisms of 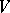 transitively permutes the totally-isotropic subspaces of the same dimension and that all maximal totally-isotropic subspaces in
transitively permutes the totally-isotropic subspaces of the same dimension and that all maximal totally-isotropic subspaces in 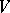 have the same dimension (the Witt index of
have the same dimension (the Witt index of 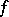 ). A second consequence of Witt's theorem may be stated as follows: The isometry classes of non-degenerate symmetric bilinear forms of finite rank over
). A second consequence of Witt's theorem may be stated as follows: The isometry classes of non-degenerate symmetric bilinear forms of finite rank over 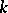 with direct orthogonal sum form a monoid with cancellation; the canonical mapping of this monoid into its Grothendieck group is injective. The group
with direct orthogonal sum form a monoid with cancellation; the canonical mapping of this monoid into its Grothendieck group is injective. The group  is called the Witt–Grothendieck group
is called the Witt–Grothendieck group 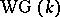 of
of 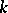 ; the tensor product of forms induces on it the structure of a ring, which is known as the Witt–Grothendieck of
; the tensor product of forms induces on it the structure of a ring, which is known as the Witt–Grothendieck of 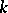 [7].
[7].
For other applications of Witt's theorem see Witt decomposition; Witt ring.
References
| [1] | E. Witt, "Theorie der quadratischen formen in beliebigen Körpern" J. Reine Angew. Math. , 176 (1937) pp. 31–44 |
| [2] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , Elements of mathematics , 1 , Addison-Wesley (1974) pp. Chapts. 1–2 (Translated from French) |
| [3] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
| [4] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [5] | E. Artin, "Geometric algebra" , Interscience (1957) |
| [6] | J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French) |
| [7] | J. Milnor, "Algebraic 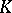 -theory and quadratic forms" Invent. Math. , 9 (1969/70) pp. 318–344 -theory and quadratic forms" Invent. Math. , 9 (1969/70) pp. 318–344 |
Witt theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Witt_theorem&oldid=16773