Logarithmic summation method
From Encyclopedia of Mathematics
One of the methods for summing series of numbers. A series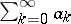 
with partial sums 
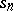is summable by the logarithmic method to the sum 
if the logarithmic mean
 |
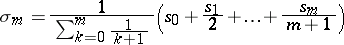converges to 
as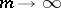 
. The logarithmic summation method is the Riesz summation method 
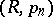with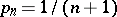 
. It is equivalent to and compatible (cf. Compatibility of summation methods) with the Riesz summation method 
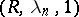with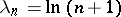 
and is more powerful than the summation method of arithmetical averages (cf. Arithmetical averages, summation method of).
References
| [1] | F. Riesz, "Sur la sommation des séries de Dirichlet" C.R. Acad. Sci. Paris , 149 (1909) pp. 18–21 |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
How to Cite This Entry:
Logarithmic summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logarithmic_summation_method&oldid=16767
Logarithmic summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logarithmic_summation_method&oldid=16767
This article was adapted from an original article by I.I. Volkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article