Adjoint operator
A linear operator 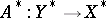 (where
(where 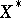 and
and 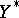 are the strong duals of locally convex spaces
are the strong duals of locally convex spaces 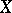 and
and 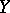 , respectively), constructed from a linear operator
, respectively), constructed from a linear operator 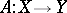 in the following way. Let the domain of definition
in the following way. Let the domain of definition 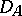 of
of 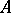 be everywhere dense in
be everywhere dense in 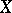 . If for all
. If for all 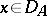 ,
,
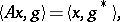 | (*) |
where 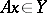 ,
, 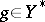 and
and 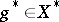 , then
, then 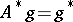 is a uniquely defined operator from the set
is a uniquely defined operator from the set 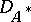 of elements
of elements 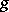 satisfying (*) into
satisfying (*) into 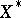 . If
. If 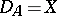 and
and 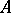 is continuous, then
is continuous, then 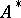 is also continuous. If, in addition,
is also continuous. If, in addition, 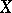 and
and 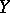 are normed linear spaces, then
are normed linear spaces, then 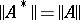 . If
. If 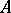 is completely continuous, then so is
is completely continuous, then so is 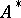 . Adjoint operators are of particular interest in the case when
. Adjoint operators are of particular interest in the case when 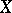 and
and 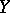 are Hilbert spaces.
are Hilbert spaces.
References
| [1] | K. Yosida, "Functional analysis" , Springer (1980) |
| [2] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
Comments
In Western literature the adjoint operator as defined above is usually called the dual or conjugate operator. The term adjoint operator is reserved for Hilbert spaces, in which case it is defined by
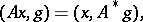 |
where 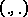 denotes the Hilbert space inner product.
denotes the Hilbert space inner product.
References
| [a1] | A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980) |
Adjoint operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjoint_operator&oldid=16759