Primitive element in a co-algebra

Let be a co-algebra over . An element is called group like if . An element is called primitive over the group-like element if , [a2], p. 199. Let be a bi-algebra (see Hopf algebra) and let be the set of primitive elements over the group-like element 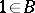of , considered as a co-algebra. Then 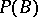becomes a Lie algebra under the commutator bracket

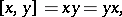(using the multiplication of ). This is the Lie algebra of primitive elements.

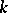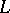For a field of characteristic zero, the functors , the universal enveloping algebra of the Lie algebra , and 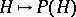, where 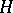is a Hopf algebra (or bi-algebra) over , establish an equivalence between the category of Lie algebras and the category of co-commutative irreducible bi-algebras (such bi-algebras are automatically Hopf algebras).

In particular, 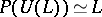, 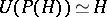for such a bi-algebra (Hopf algebra) [a2], [a1]; for the graded version of this correspondence, see Hopf algebra and the references quoted there. See also Lie polynomial for the concrete case that 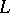is a free Lie algebra (cf. Lie algebra, free) on a set 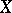and 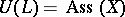is the free associative algebra over .

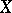References

[a1]	E. Abe, "Hopf algebras" , Cambridge Univ. Press (1977)
[a2]	M.E. Sweedler, "Hopf algebras" , Benjamin (1963)