Simple-iteration method
A method for approximately solving a system of linear algebraic equations  that can be transformed to the form
that can be transformed to the form  and whose solution is looked for as the limit of a sequence
and whose solution is looked for as the limit of a sequence  ,
,  where
where  is an initial approximation. In order that the simple-iteration method converges for any initial approximation
is an initial approximation. In order that the simple-iteration method converges for any initial approximation  it is necessary and sufficient that all eigenvalues of
it is necessary and sufficient that all eigenvalues of  are less than one in modulus; it is sufficient that some norm of
are less than one in modulus; it is sufficient that some norm of  is less than one. If in some norm, compatible with the norm of a vector
is less than one. If in some norm, compatible with the norm of a vector  ,
, 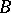 satisfies
satisfies 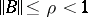 , then the simple-iteration method converges at the rate of a geometric series and the estimate
, then the simple-iteration method converges at the rate of a geometric series and the estimate
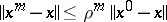 |
holds for its error.
In the case of a cubic, octahedral or spherical vector norm, the condition 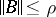 is fulfilled if
is fulfilled if
1) 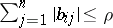 ,
, 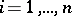 ;
;
2) 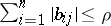 ,
, 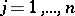 ;
;
3)  .
.
The simplest version of the method corresponds to the case when one takes 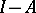 , where
, where 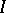 is the identity matrix, for
is the identity matrix, for  . If all diagonal entries of
. If all diagonal entries of 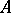 are non-zero, then, choosing
are non-zero, then, choosing  and
and 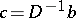 , where
, where 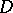 is the diagonal matrix with as diagonal entries those of
is the diagonal matrix with as diagonal entries those of 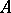 , one obtains the Jacobi method or the method of simultaneous displacement.
, one obtains the Jacobi method or the method of simultaneous displacement.
A particular case of the simple-iteration method is the method with 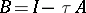 and
and 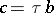 , where
, where  is an iteration parameter, chosen from the condition that the norm of
is an iteration parameter, chosen from the condition that the norm of 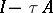 is minimal with respect to
is minimal with respect to  . If
. If 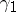 and
and 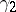 are the minimal and maximal eigenvalues of a symmetric positive-definite matrix
are the minimal and maximal eigenvalues of a symmetric positive-definite matrix  and
and 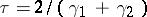 , then one has for the matrix
, then one has for the matrix  in the spherical norm the estimate
in the spherical norm the estimate  , with
, with  .
.
For a system of non-linear algebraic equations
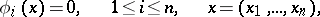 |
the simple-iteration method has the form
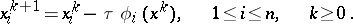 |
The problem of choosing the iteration parameter  is solved in dependence on the differentiability properties of the
is solved in dependence on the differentiability properties of the 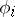 . Often it is subjected to the requirement that the method converges locally in a neighbourhood of a solution.
. Often it is subjected to the requirement that the method converges locally in a neighbourhood of a solution.
References
| [1] | D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian) |
| [2] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
| [3] | J.M. Ortega, W.C. Rheinboldt, "Iterative solution of non-linear equations in several variables" , Acad. Press (1970) |
| [4] | A.A. Samarskii, E.S. Nikolaev, "Numerical methods for grid equations" , 1–2 , Birkhäuser (1989) (Translated from Russian) |
Simple-iteration method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simple-iteration_method&oldid=16747