Luzin-N-property
"null-propertynull-property" , of a function 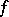 , continuous on an interval
, continuous on an interval 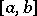
For any set 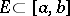 of measure
of measure 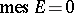 , the image of this set,
, the image of this set, 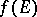 , also has measure zero. It was introduced by N.N. Luzin in 1915 (see [1]). The following assertions hold.
, also has measure zero. It was introduced by N.N. Luzin in 1915 (see [1]). The following assertions hold.
1) A function 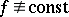 on
on 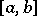 such that
such that  almost-everywhere on
almost-everywhere on 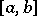 does not have the Luzin
does not have the Luzin 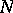 -property.
-property.
2) If 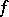 does not have the Luzin
does not have the Luzin 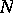 -property, then on
-property, then on 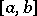 there is a perfect set
there is a perfect set  of measure zero such that
of measure zero such that 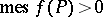 .
.
3) An absolutely continuous function has the Luzin 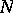 -property.
-property.
4) If 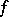 has the Luzin
has the Luzin 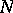 -property and has bounded variation on
-property and has bounded variation on 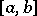 (as well as being continuous on
(as well as being continuous on 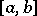 ), then
), then 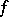 is absolutely continuous on
is absolutely continuous on 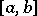 (the Banach–Zaretskii theorem).
(the Banach–Zaretskii theorem).
5) If 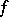 does not decrease on
does not decrease on 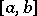 and
and 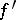 is finite on
is finite on 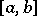 , then
, then 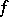 has the Luzin
has the Luzin 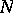 -property.
-property.
6) In order that 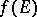 be measurable for every measurable set
be measurable for every measurable set 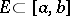 it is necessary and sufficient that
it is necessary and sufficient that 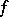 have the Luzin
have the Luzin 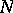 -property on
-property on 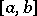 .
.
7) A function 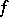 that has the Luzin
that has the Luzin 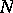 -property has a derivative
-property has a derivative 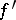 on the set for which any non-empty portion of it has positive measure.
on the set for which any non-empty portion of it has positive measure.
8) For any perfect nowhere-dense set 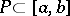 there is a function
there is a function 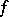 having the Luzin
having the Luzin  -property on
-property on 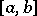 and such that
and such that 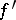 does not exist at any point of
does not exist at any point of 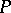 .
.
The concept of Luzin's 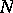 -property can be generalized to functions of several variables and functions of a more general nature, defined on measure spaces.
-property can be generalized to functions of several variables and functions of a more general nature, defined on measure spaces.
References
| [1] | N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1915) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212) |
Comments
There is another property intimately related to the Luzin 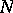 -property. A function
-property. A function 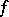 continuous on an interval
continuous on an interval 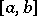 has the Banach
has the Banach 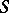 -property if for all Lebesgue-measurable sets
-property if for all Lebesgue-measurable sets 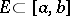 and all
and all 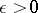 is a
is a 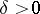 such that
such that
 |
This is clearly stronger than the 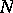 -property. S. Banach proved that a function
-property. S. Banach proved that a function 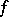 has the
has the 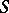 -property (respectively, the
-property (respectively, the 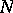 -property) if and only if (respectively, only if — see below for the missing "if" ) the inverse image
-property) if and only if (respectively, only if — see below for the missing "if" ) the inverse image 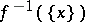 is finite (respectively, is at most countable) for almost-all
is finite (respectively, is at most countable) for almost-all  in
in 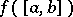 . For classical results on the
. For classical results on the 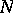 - and
- and  -properties, see [a3].
-properties, see [a3].
Recently a powerful extension of these results has been given by G. Mokobodzki (cf. [a1], [a2]), allowing one to prove deep results in potential theory. Let  and
and 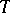 be two compact metrizable spaces,
be two compact metrizable spaces,  being equipped with a probability measure
being equipped with a probability measure  . Let
. Let 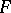 be a Borel subset of
be a Borel subset of  and, for any Borel subset
and, for any Borel subset  of
of  , define the subset
, define the subset 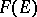 of
of 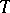 by
by  (if
(if 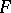 is the graph of a mapping
is the graph of a mapping 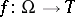 , then
, then 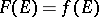 ). The set
). The set 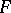 is said to have the property (N) (respectively, the property (S)) if there exists a measure
is said to have the property (N) (respectively, the property (S)) if there exists a measure 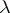 on
on 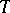 (here depending on
(here depending on 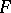 ) such that for all
) such that for all 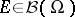 ,
,
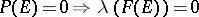 |
(respectively, for all 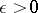 there is a
there is a 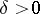 such that for all
such that for all  one has
one has
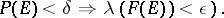 |
Now 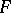 has the property (N) (respectively, the property (S)) if and only if the section
has the property (N) (respectively, the property (S)) if and only if the section 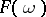 of
of  is at most countable (respectively, is finite) for almost-all
is at most countable (respectively, is finite) for almost-all 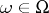 .
.
References
| [a1] | C. Dellacherie, D. Feyel, G. Mokobodzki, "Intégrales de capacités fortement sous-additives" , Sem. Probab. Strasbourg XVI , Lect. notes in math. , 920 , Springer (1982) pp. 8–28 |
| [a2] | A. Louveau, "Minceur et continuité séquentielle des sous-mesures analytiques fortement sous-additives" , Sem. Initiation à l'Analyse , 66 , Univ. P. et M. Curie (1983–1984) |
| [a3] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
| [a4] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
Luzin-N-property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Luzin-N-property&oldid=16711