Pontryagin character

The characteristic class defined by the equality , where is the complexification of the fibre bundle and is the Chern character. The Pontryagin character as an element of the ring is determined by the even series and has the following properties

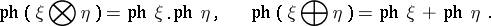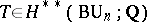The index class is defined to be equal to , where is the Todd class. The index class 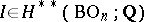is expressed in Wu generators (see Characteristic class) by the formula

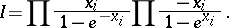The following theorem on the relationship between the Pontryagin class and the 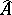-class holds (cf. Pontryagin class). Let 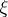be a real vector bundle over the base 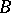with a 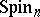-structure, 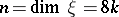. For such bundles there is the Thom isomorphism in real 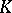-theory:

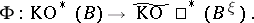Let

be the Thom isomorphism, which is uniquely determined by the orientation of the bundle 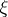. Then

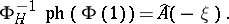This formula is an exact analogue of the corresponding statement on the relationship between the Chern character and the Todd class.

If 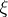is a complex vector bundle, then 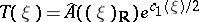. Here 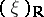is the real part of the bundle, and 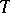is the Todd class.

For references see Pontryagin class.